题目内容
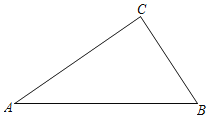
【题目】如图,在Rt△ABC中,∠ACB=90°,两直角边AC=8cm,BC=6cm.
(1)作∠BAC的平分线AD交BC于点D;(尺规作图,不写作法,保留作图痕迹)
(2)计算△ABD的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)利用尺规作出∠CAB的角平分线即可;
(2)作DE⊥AB,垂足为E.设CD=DE=x,在Rt△DEB中,利用勾股定理构建方程即可解决问题.
解:(1)作图如下:
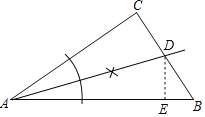
AD是∠ABC的平分线.
(2)在Rt△ABC中,由勾股定理得:
AB=![]() =
=![]() =10,
=10,
作DE⊥AB,垂足为E.
∵∠ACB=90°,AD是∠ABC的平分线,
∴CD=DE,
设CD=DE=x,
∴DB=6﹣x,
∵∠C=∠AED=90°,AD=AD,DC=DE,
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE=8,
∴EB=AB﹣AE=10﹣8=2,
在Rt△DBE中由勾股定理得:x2+22=(6﹣x)2
解方程得x=![]() ,
,
∴S=![]() ABDE
ABDE![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目