题目内容
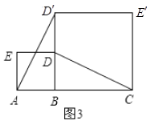
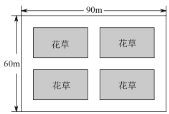
【题目】成都市中心城区“小游园，微绿地”规划已经实施，武侯区某街道有一块矩形空地进入规划试点．如图，已知该矩形空地长为
，宽为
，按照规划将预留总面积为
的四个小矩形区域（阴影部分）种植花草，并在花草周围修建三条横向通道和三条纵向通道，各通道的宽度相等．
（1）求各通道的宽度；
（2）现有一工程队承接了对这的区域（阴影部分）进行种植花草的绿化任务，该工程队先按照原计划进行施工，在完成了
的绿化任务后，将工作效率提高
，结果提前
天完成任务，求该工程队原计划每天完成多少平方米的绿化任务？
【答案】（1）各通道的宽度为
米；（2）原计划每天完成
平方米的绿化任务.
【解析】
（1）设各通道的宽度为x米，将四个小矩形合并成一个大矩形，则大矩形的长为(90-3x)cm，宽为(60-3x)cm，再根据矩形面积公式列方程求解即可；
（2）设该工程队原计划每天完成ym2的绿化任务，则按原计划完成任务需要
天，完成
的绿化任务需要
天，提高工作效率后完成剩余工作量所需要的时间为
天，再按照题干所给时间关系列出方程并求解即可.
解：（1）设各通道的宽度为x米，将四个小矩形合并成一个大矩形，则可得方程，
(90-3x)(60-3x)=4536，解得x=2或48(不合题意，舍去)，
故各通道的宽度为米；
（2）设该工程队原计划每天完成ym2的绿化任务，则由题干条件得，
，解得y=400m2/天，
经检验，y=400m2/天是原方程的解，并符合题意，
故原计划每天完成平方米的绿化任务.
练习册系列答案
相关题目
