ЬтФПФкШн
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§![]() КЭЗДБШР§КЏЪ§
КЭЗДБШР§КЏЪ§![]() ЃЎ
ЃЎ
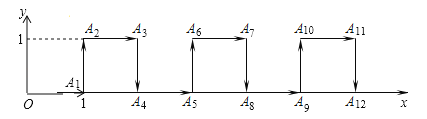
![]() ШчЭМ1ЃЌШє
ШчЭМ1ЃЌШє![]() ЃЌЧвКЏЪ§
ЃЌЧвКЏЪ§![]() ЁЂ
ЁЂ![]() ЕФЭМЯѓЖМОЙ§Еу
ЕФЭМЯѓЖМОЙ§Еу![]() ЃЎЧѓmЃЌkЕФжЕЃЛ
ЃЎЧѓmЃЌkЕФжЕЃЛ
![]() ШчЭМ2ЃЌЙ§Еу
ШчЭМ2ЃЌЙ§Еу![]() зїyжсЕФЦНааЯпlгыКЏЪ§
зїyжсЕФЦНааЯпlгыКЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕуBЃЌгыЗДБШР§КЏЪ§
ЕФЭМЯѓЯрНЛгкЕуBЃЌгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕуCЃЎ
ЕФЭМЯѓЯрНЛгкЕуCЃЎ
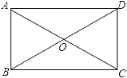
![]() Шє
Шє![]() ЃЌжБЯпlгыКЏЪ§
ЃЌжБЯпlгыКЏЪ§![]() ЕФЭМЯѓЯрНЛЕу
ЕФЭМЯѓЯрНЛЕу![]() ЕБЕуBЁЂCЁЂDжаЕФвЛЕуЕНСэЭтСНЕуЕФОрРыЯрЕШЪБЃЌЧѓ
ЕБЕуBЁЂCЁЂDжаЕФвЛЕуЕНСэЭтСНЕуЕФОрРыЯрЕШЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
![]() Й§ЕуBзїxжсЕФЦНааЯпгыКЏЪ§
Й§ЕуBзїxжсЕФЦНааЯпгыКЏЪ§![]() ЕФЭМЯѓЯрНЛгыЕу
ЕФЭМЯѓЯрНЛгыЕу![]() ЕБ
ЕБ![]() ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪЕЪ§ЪБЃЌЕуBЁЂCМфЕФОрРыгыЕуBЁЂEМфЕФОрРыжЎКЭdЪМжеЪЧвЛИіЖЈжЕЃЎЧѓДЫЪБkЕФжЕМАЖЈжЕdЃЎ
ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪЕЪ§ЪБЃЌЕуBЁЂCМфЕФОрРыгыЕуBЁЂEМфЕФОрРыжЎКЭdЪМжеЪЧвЛИіЖЈжЕЃЎЧѓДЫЪБkЕФжЕМАЖЈжЕdЃЎ
ЁОД№АИЁПЃЈ1ЃЉm=12ЃЌk=2ЃЛЃЈ2ЃЉЂйm-n=1Лђm-n=4ЃЛЂкk=1ЃЌЖЈжЕd=1
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНМДПЩЧѓНтЃЌНЋЕуAЕФзјБъДњШыЗДБШР§КЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЂйBDЃН2+nЉmЃЌBCЃНmЉnЃЌDCЃН2+nЉnЃН2ЃЌгЩBDЃНBCЛђBDЃНDCЛђBCЃНCDЕУЃКmЉnЃН1Лђ0Лђ2ЃЌМДПЩЧѓНтЃЛ
ЂкЕуEЕФзјБъЮЊЃЈ![]() ЃЌmЃЉЃЌdЃНBC+BEЃНmЉn+ЃЈ1Љ
ЃЌmЃЉЃЌdЃНBC+BEЃНmЉn+ЃЈ1Љ![]() ЃЉЃН1+ЃЈmЉnЃЉЃЈ1Љ
ЃЉЃН1+ЃЈmЉnЃЉЃЈ1Љ![]() ЃЉЃЌМДПЩЧѓНтЃЎ
ЃЉЃЌМДПЩЧѓНтЃЎ
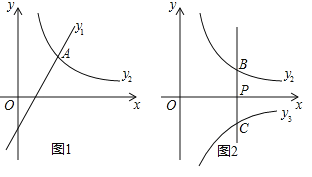
НтЃКЃЈ1ЃЉЕБnЃНЉ2ЪБЃЌy1ЃНkxЉ2ЃЌ
НЋЕуAЃЈ3ЃЌ4ЃЉДњШывЛДЮКЏЪ§y1ЃНkxЉ2
ЕУЃК3kЉ2ЃН4ЃЌ
НтЕУЃКkЃН2ЃЌ
НЋЕуAЃЈ3ЃЌ4ЃЉДњШыЗДБШР§КЏЪ§ЕУЃКmЃН3ЁС4ЃН12ЃЛ
ЁрmЃН12ЃЌkЃН2ЃЛ
ЃЈ2ЃЉЂйЕБxЃН1ЪБЃЌЕуDЁЂBЁЂCЕФзјБъЗжБ№ЮЊЃЈ1ЃЌ2+nЃЉЁЂЃЈ1ЃЌmЃЉЁЂЃЈ1ЃЌnЃЉЃЌ
дђBDЃН|2+nЉm|ЃЌBCЃНmЉnЃЌDCЃН2+nЉnЃН2
дђBDЃНBCЛђBDЃНDCЛђBCЃНCDЃЌ
МДЃК|2+nЉm|ЃНmЉnЛђ|2+nЉm|ЃН2ЛђmЉnЃН2ЃЌ
МДЃКmЉnЃН1Лђ0Лђ2Лђ4ЃЌ
ЕБmЉnЃН0ЪБЃЌmЃНnгыЬтвтВЛЗћЃЌ
ЕуDВЛФмдкCЕФЯТЗНЃЌМДBCЃНCDвВВЛДцдкЃЌn+2ЃОnЃЌЙЪmЉnЃН2ВЛГЩСЂЃЌ
ЙЪmЉnЃН1ЛђmЉnЃН4ЃЛ
ЂкЕуEЕФКсзјБъЮЊЃК![]() ЃЌ
ЃЌ
ЕБЕуEдкЕуBзѓВрЪБЃЌ
dЃНBC+BEЃНmЉn+ЃЈ1Љ![]() ЃЉЃН1+ЃЈmЉnЃЉЃЈ1Љ
ЃЉЃН1+ЃЈmЉnЃЉЃЈ1Љ![]() ЃЉЃЌ
ЃЉЃЌ
mЉnЕФжЕШЁВЛДѓгк1ЕФШЮвтЪ§ЪБЃЌdЪМжеЪЧвЛИіЖЈжЕЃЌ
ЕБ1Љ![]() ЃН0ЪБЃЌДЫЪБkЃН1ЃЌДгЖјdЃН1ЃЎ
ЃН0ЪБЃЌДЫЪБkЃН1ЃЌДгЖјdЃН1ЃЎ
ЕБЕуEдкЕуBгвВрЪБЃЌ
ЭЌРэBC+BEЃНЃЈmЉnЃЉЃЈ1+![]() ЃЉЉ1ЃЌ
ЃЉЉ1ЃЌ
ЕБ1+![]() ЃН0ЃЌkЃНЉ1ЪБЃЌЃЈВЛКЯЬтвтЩсШЅЃЉ
ЃН0ЃЌkЃНЉ1ЪБЃЌЃЈВЛКЯЬтвтЩсШЅЃЉ
ЙЪkЃН1ЃЌdЃН1ЃЎ

ЁОЬтФПЁПЮЊСЫНтФГаЃбЇЩњЕФЩэИпЧщПіЃЌЭѕРЯЪІЫцЛњГщШЁИУаЃФаЩњЁЂХЎЩњНјааГщбљЕїВщЃЌвбжЊГщШЁЕФбљБОжаЃЌФаЩњЁЂХЎЩњШЫЪ§ЯрЭЌЃЌРћгУЫљЕУЪ§ОнЛцжЦШчЯТЭГМЦЭМБэЃК
зщБ№ | ЩэИп |
|
|
|
|
|
|
|
|
|
|
ЩэИпЧщПіЗжзщБэ
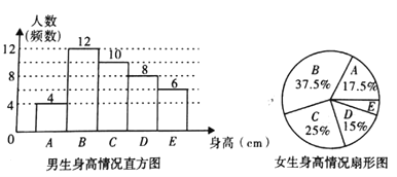
ИљОнЭМБэЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉбљБОжаЃЌХЎЩњЩэИпдк![]() зщЕФШЫЪ§га_________ШЫЃЛ
зщЕФШЫЪ§га_________ШЫЃЛ
ЃЈ2ЃЉдкЩЯУцЕФЩШаЮЭГМЦЭМжаЃЌБэЪО![]() зщЕФЩШаЮЕФдВаФНЧЪЧ_________ЁуЃЛ
зщЕФЩШаЮЕФдВаФНЧЪЧ_________ЁуЃЛ
ЃЈ3ЃЉвбжЊИУаЃЙВгаФаЩњ800ШЫЃЌХЎЩњ760ШЫЃЌЧыЙРМЦИУаЃЩэИпдк![]() жЎМфЕФбЇЩњдМгаЖрЩйШЫЃП
жЎМфЕФбЇЩњдМгаЖрЩйШЫЃП