题目内容
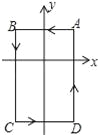
【题目】将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中，点O为坐标原点，点C、A分别在x、y轴的正半轴上，一条抛物线经过点A、C及点B（﹣3，0）．
（1）求该抛物线的解析式；
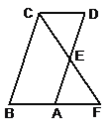
（2）若点P是线段BC上一动点，过点P作AB的平行线交AC于点E，连接AP，当△APE的面积最大时，求点P的坐标；
（3）在第一象限内的该抛物线上是否存在点G，使△AGC的面积与（2）中△APE的最大面积相等？若存在，请求出点G的坐标；若不存在，请说明理由．
【答案】
（1）
解：如图，
∵抛物线y=ax2+bx+c（a≠0）的图象经过点A（0，6），
∴c=6．
∵抛物线的图象又经过点（﹣3，0）和（6，0），
∴ 
，
解之得 
，
故此抛物线的解析式为：y=﹣ 
x2+x+6．
（2）解：设点P的坐标为（m，0），
则PC=6﹣m，S△ABC= 
BCAO= ×9×6=27；
∵PE∥AB，
∴△CEP∽△CAB；
∴ 
，
即 
=（ 
）2，
∴S△CEP= （6﹣m）2，
∵S△APC= PCAO= （6﹣m）×6=3（6﹣m），
∴S△APE=S△APC﹣S△CEP=3（6﹣m）﹣ （6﹣m）2=﹣ （m﹣ 
）2+ 
；
当m= 时，S△APE有最大面积为 ；
此时，点P的坐标为（ ，0）．
（3）
解：如图，过G作GH⊥BC于点H，设点G的坐标为G（a，b），
连接AG、GC，
∵S梯形AOHG= a（b+6），
S△CHG= （6﹣a）b，
∴S四边形AOCG= a（b+6）+ （6﹣a）b=3（a+b）．
∵S△AGC=S四边形AOCG﹣S△AOC ，
∴ =3（a+b）﹣18，
∵点G（a，b）在抛物线y=﹣ x2+x+6的图象上，
∴b=﹣ a2+a+6，
∴ =3（a﹣ a2+a+6）﹣18，
化简，得4a2﹣24a+27=0，
解之得a1= ，a2= 
；
故点G的坐标为（ ， ）或（ ， 
）．
【解析】（1）已知OA、OC的长，可得A、C的坐标，即可用待定系数法求出抛物线的解析式．（2）设出点P的横坐标，表示出CP的长，由于PE∥AB，可利用相似三角形△CPE∽△CBA，求出△APE的面积表达式，进而可将面积问题转换为二次函数的最值问题，根据函数的性质即可得到△APE的最大面积及对应的P点坐标．（3）由于△AGC的面积无法直接求出，可用割补法求解，过G作GH⊥x轴于H，设出G点坐标，表示出△HGC、梯形AOHG的面积，它们的面积和减去△AOC的面积即可得到△AGC的面积表达式，然后将（2）题所得△APE的面积最大值代入上式中，联立抛物线的解析式即可得到点G的坐标．
