题目内容
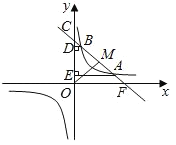
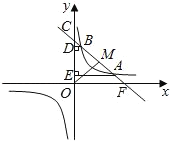
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 且
且![]() )的图象在第一象限交于点
)的图象在第一象限交于点![]() 、
、![]() ,且该一次函数的图象与
,且该一次函数的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() .已知
.已知![]() ,
,![]() .
.
(1)求![]() 的值和反比例函数的解析式;
的值和反比例函数的解析式;
(2)若点![]() 为一次函数图象上的动点,求
为一次函数图象上的动点,求![]() 长度的最小值.
长度的最小值.
【答案】(1)![]() 的值为4或-1;
的值为4或-1;![]() ;(2)
;(2)![]() .
.
【解析】
(1)将点![]() 代入
代入![]() ,即可求出
,即可求出![]() 的值,进一步可求出反比例函数解析式;
的值,进一步可求出反比例函数解析式;
(2)先证![]() ,由
,由![]() 可求出
可求出![]() 的长度,可进一步求出点
的长度,可进一步求出点![]() 的坐标,然后利用待定系数法求出直线
的坐标,然后利用待定系数法求出直线![]() 的解析式,即可求出直线
的解析式,即可求出直线![]() 与坐标轴交点C、F的坐标,进而可判断△COF的形状,再利用垂线段最短即可求出
与坐标轴交点C、F的坐标,进而可判断△COF的形状,再利用垂线段最短即可求出![]() 长度的最小值.
长度的最小值.
解:(1)将点![]() 代入
代入![]() ,得,
,得,![]() ,解得,
,解得,![]() ,
,![]() ,
,
∴![]() 的值为4或-1;反比例函数解析式为:
的值为4或-1;反比例函数解析式为:![]() ;
;
(2)∵![]() 轴,
轴,![]() 轴,∴
轴,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
得:![]() ,解得,
,解得,![]() ,
,![]() ,
,
∴![]() ,
,
设直线![]() 与
与![]() 轴交点为
轴交点为![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时
时![]() ,∴
,∴![]() ,
,![]() ,则
,则![]() ,
,
∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
则当![]() 垂直
垂直![]() 于
于![]() 时,由垂线段最短可知,
时,由垂线段最短可知,![]() 有最小值,
有最小值,
此时![]() .
.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目