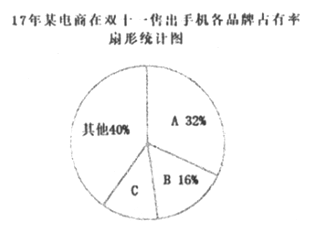
题目内容
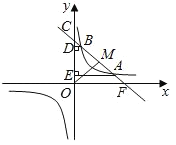
【题目】如图,已知抛物线的方程y=- ![]() (x+2)(x-m) (m>0)与x轴交于B、C,与y轴交于点E,且点B在点C的左侧,抛物线还经过点P(2,2)
(x+2)(x-m) (m>0)与x轴交于B、C,与y轴交于点E,且点B在点C的左侧,抛物线还经过点P(2,2)
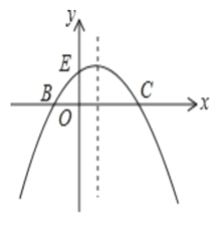
(1)求该抛物线的解析式
(2)在(1)的条件下,求△BCE的面积
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使EH+BH的值最小。求出点H的坐标。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)直接带入P点坐标求出m即可;(2)由(1)求出的函数关系式,解出函数与x,y轴的交点坐标,即可求出三角形面积;(3)作E关于抛物线对称轴的对称点F,连接BF交y轴于点H,由两点之间线段最短可得最小值。
(1)解:将P点代入函数式得:![]()
解得: m=4,
∴ 该抛物线的解析式为: ![]() .
.
(2)解: 由(1)得-![]() (x+2)(x-4)=0,
(x+2)(x-4)=0,
解得x=-2或x=4,
∴B(-2,0),C(4,0),
∴BC=4-(-2)=6,
当x=0, y=2,
∴OE=2.
∴![]()
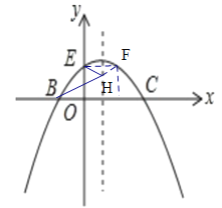
(3)解: 如图,作E关于抛物线对称轴的对称点F,连接BF交y轴于点H,
∵![]() ,
,
则F(2,2),
EH+BH=FH+HB=FB,
设直线FB的解析式为:y=kx+b,
∴![]()
解得: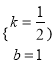 ,
,
故y=![]() ,
,
当x=1, y=![]() ×1+1=
×1+1=![]() ,
,
∴H(1,![]() ).
).

练习册系列答案
相关题目