题目内容
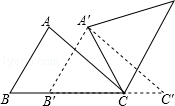
在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为 ,且
,且 ,连接AD、BD.
,连接AD、BD.
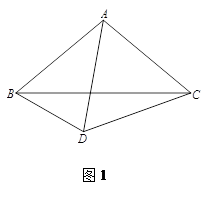
(1)如图1,当∠BAC=100°, 时,∠CBD 的大小为_________;
时,∠CBD 的大小为_________;
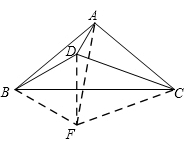
(2)如图2,当∠BAC=100°, 时,求∠CBD的大小;
时,求∠CBD的大小;
(3)已知∠BAC的大小为m( ),若∠CBD 的大小与(2)中的结果相同,请直接写出
),若∠CBD 的大小与(2)中的结果相同,请直接写出 的大小.
的大小.

 ,且
,且 ,连接AD、BD.
,连接AD、BD.(1)如图1,当∠BAC=100°,
 时,∠CBD 的大小为_________;
时,∠CBD 的大小为_________;(2)如图2,当∠BAC=100°,
 时,求∠CBD的大小;
时,求∠CBD的大小;(3)已知∠BAC的大小为m(
 ),若∠CBD 的大小与(2)中的结果相同,请直接写出
),若∠CBD 的大小与(2)中的结果相同,请直接写出 的大小.
的大小.

(1)30°;(2)30°;(3)α=120°-m°,α=60°或α=240-m°.
试题分析:(1)由∠BAC=100°,AB=AC,可以确定∠ABC=∠ACB=40°,旋转角为α,α=60°时△ACD是等边三角形,且AC=AD=AB=CD,知道∠BAD的度数,进而求得∠CBD的大小.
(2)由∠BAC=100°,AB=AC,可以确定∠ABC=∠ACB=40°,连结DF、BF.AF=FC=AC,∠FAC=∠AFC=60°,∠ACD=20°,由∠DCB=20°案.依次证明△DCB≌△FCB,△DAB≌△DAF.利用角度相等可以得到答案.
(3)结合(1)(2)的解题过程可以发现规律,求得答案.
试题解析:(1)30°;(2)30°;
(2)如图作等边△AFC,连结DF、BF.
∴AF=FC=AC,∠FAC=∠AFC=60°.
∵∠BAC=100°,AB=AC,∴∠ABC=∠BCA=40°.
∵∠ACD=20°,∴∠DCB=20°.
∴∠DCB=∠FCB=20°.①
∵AC=CD,AC=FC,∴DC=FC.②
∵BC=BC,③
∴由①②③,得△DCB≌△FCB,
∴DB=BF,∠DBC=∠FBC.
∵∠BAC=100°,∠FAC=60°,∴∠BAF=40°.
∵∠ACD=20°,AC=CD,∴∠CAD=80°.∴∠DAF=20°.
∴∠BAD=∠FAD=20°.④
∵AB=AC,AC=AF,∴AB=AF.⑤
∵AD=AD,⑥
∴由④⑤⑥,得△DAB≌△DAF.∴FD=BD.∴FD=BD=FB.∴∠DBF=60°.∴∠CBD=30°.
(3)α=120°-m°,α=60°或α=240-m°.

练习册系列答案
相关题目
 ,设c为最长边.当
,设c为最长边.当 时,△ABC是直角三角形;当
时,△ABC是直角三角形;当 时,利用代数式
时,利用代数式 和
和 的大小关系,可以判断△ABC的形状(按角分类).
的大小关系,可以判断△ABC的形状(按角分类). 时,△ABC为锐角三角形;当
时,△ABC为锐角三角形;当 时,△ABC为钝角三角形.” 请你根据小明的猜想完成下面的问题:
时,△ABC为钝角三角形.” 请你根据小明的猜想完成下面的问题: ,
, 时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形? ).
).


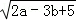 +(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
+(2a+3b﹣13)2=0,则此等腰三角形的周长为( )