题目内容
已知抛物线y=4x2-8x-1.
(1)求它的顶点坐标;
(2)求它与x轴、y轴的交点坐标.
解:(1)∵y=4x2-8x-1,
∴y=4(x2-2x)-1,
=4(x-1)2-5,
∴顶点坐标(1,-5);
(2)令y=0,即4x2-8x-1=0,
∴ ,
,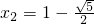 ,
,
∴它与x轴的交点坐标是( ,0),(
,0),(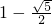 ,0),
,0),
令x=0,则y=-1,
∴它与y轴的交点坐标是(0,-1).
分析:(1)将二次函数配方后确定其顶点坐标即可,也可以代入求顶点坐标的公式中求顶点坐标;
(2)分别令x=0和令y=0求得y与x的值分别作为与y轴和与x轴的交点坐标.
点评:本题考查了二次函数的顶点坐标和求与坐标轴的交点坐标问题,此类题目往往是解决二次函数综合题的关键和基础,常常不单独考查.
∴y=4(x2-2x)-1,
=4(x-1)2-5,
∴顶点坐标(1,-5);
(2)令y=0,即4x2-8x-1=0,
∴
 ,
,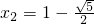 ,
,∴它与x轴的交点坐标是(
 ,0),(
,0),(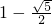 ,0),
,0),令x=0,则y=-1,
∴它与y轴的交点坐标是(0,-1).
分析:(1)将二次函数配方后确定其顶点坐标即可,也可以代入求顶点坐标的公式中求顶点坐标;
(2)分别令x=0和令y=0求得y与x的值分别作为与y轴和与x轴的交点坐标.
点评:本题考查了二次函数的顶点坐标和求与坐标轴的交点坐标问题,此类题目往往是解决二次函数综合题的关键和基础,常常不单独考查.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目