Question

已知抛物线y=4x²-7x+4与直线y=x+b相交于A、B两点．
（1）求b的取值范围；
（2）当AB=2时，求b的值；
（3）设坐标原点为O，在（2）的条件下，求△AOB的面积．

Answer 1

分析：（1）根据交点的意义可得4x²-7x+4=x+b，整理，得4x²-8x+（4-b）=0，抛物线与直线有两个交点，即方程有两个不相等的实数根，即△=（-8）²-16（4-b）=16b＞0，所以b＞0．
（2）设A（x₁，y₁）B（x₂，y₂），x₁＜x₂，根据x₁、x₂是方程4x²-8x+（4-b）=0的两根，利用根与系数的关系可知
|x₁-x₂|=

b

，根据题意可知y₂-y₁=x₂-x₁，所以AB=

(x2-x1)2+(y2-y1)2

=

2

|x2-x1|=

2b

=2，即b=2．
（3）由（2）可知，直线的解析式为y=x+2，设直线与y轴交于C点，则C点的坐标为（0，2），OC=2，易知x₂＞x₁＞0，用点的坐标表示出线段的长度，并表示出S_△AOC，S_△BOC，可知S_△AOB=S_△AOC-S_△BOC=

b

=

2

．

解答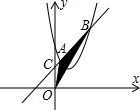：解：（1）根据题意，得4x²-7x+4=x+b．（1分）
整理，得4x²-8x+（4-b）=0．（2分）
∵抛物线与直线有两个交点，
∴△=（-8）²-16（4-b）=16b＞0．
∴b＞0（3分）．

（2）不妨设A（x₁，y₁）B（x₂，y₂），x₁＜x₂，如图
∵x₁、x₂是方程4x²-8x+（4-b）=0的两根
∴x1+x2=2，x1x2=

4-b

4

（4分）
∴|x2-x1|=

(x1+x2)2-4x1x2

=

22-(4-b)

=

b

（5分）
∴y₁=x₁+b，y₂=x₂+b
∴y₂-y₁=x₂-x₁（6分）
∴AB=

(x2-x1)2+(y2-y1)2

=

2

|x2-x1|=

2b

=2
∴b=2．（7分）

（3）由（2）可知，直线的解析式为y=x+2，设直线与y轴交于C点，
则C点的坐标为（0，2），OC=2，易知x₂＞x₁＞0．
∵S△AOC=

1

2

OC•x1，S△BOC=

1

2

OC•x2（8分）
∴S△AOB=S△BOC-S△AOC=

1

2

OC•(x2-x1)（9分）
=

1

2

×2|x2-x1|=|x2-x1|=

b

∴S△AOB=

2

（10分）．

点评：本题考查二次函数的综合应用，解题的关键是能利用一元二次方程解的意义和根的判别式求得b的取值范围，并会用根与系数的关系求得交点之间的关系，能熟练地运用数形结合的思想求得几何图形的面积．