Question

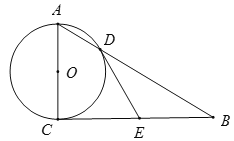
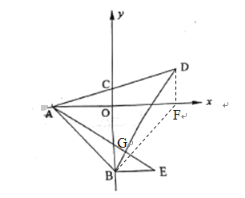
【题目】如图，已知， ，且，满足，为第一象限内一点，连接，连接交轴于点，且．

(1)求、两点的坐标；

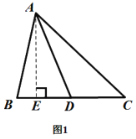
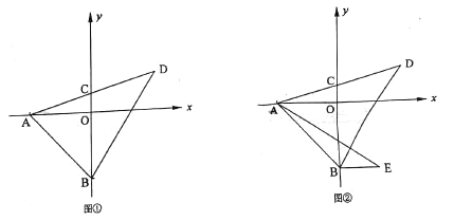
(2)如图①，若的面积为20，求点的坐标；

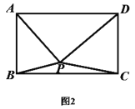
(3)如图②，在第四象限内过点作轴，且，连接．求证:， 且．

Answer 1

【答案】（1）点A坐标为（-4,0），点B的坐标为（0，-4）；（2）点D的坐标为（4,2）；（3）见解析

【解析】

（1）根据平方和绝对值的非负性即可得出结论；

（2）过点D作DE⊥y轴，利用AAS证出△DEC≌△AOC，从而得出DE=AO=4，S△DEC=S△AOC，然后根据已知面积即可求出OE的长，从而求出结论；

（3）利用SAS证出△ABE≌BFD，从而得出，∠EAB=∠DBF，然后根据三角形外角的性质和等量代换即可得出结论．

解：（1）∵，

∴

解得：a=b=-4

∴点A坐标为（-4,0），点B的坐标为（0，-4）

（2）过点D作DE⊥y轴于E

∴∠DEC=∠AOC=90°

在△DEC和△AOC中

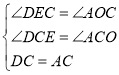
∴△DEC≌△AOC

∴DE=AO=4，S△DEC=S△AOC

∵的面积为20

∴S△AOB＋S△AOC＋S△DCB=20

∴S△AOB＋S△DEC＋S△DCB=20

∴S△AOB＋S△DEB=20

∴OA·OB＋BE·DE=20

∴×4×4＋BE×4=20

解得：BE=6

∴OE=BE－OB=2

∴点D的坐标为（4,2）

（3）过点D作DF⊥x轴于F,连接BF，设BD与AE交于点G

∴DF∥OC

∵AC=CD

∴AO=OF

∴OB垂直平分AF，DF=2OC

∴AB=BF

∴∠BAF=∠BFA

∵OA=OB，∠AOB=90°

∴∠BAF=∠OBA=45°

∴△ABF为等腰直角三角形，∠ABF=90°

∴∠ABE=135°，∠BFD=135°

∴∠ABE=∠BFD

∵

∴BE=DF

在△ABE和△BFD中

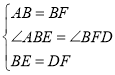
∴△ABE≌BFD

∴，∠EAB=∠DBF

∴∠BGE=∠EAB＋∠GBA=∠DBF＋∠GBA=∠ABF=90°

∴