[题目]如图.圆柱形玻璃容器高19cm.底面周长为60cm.在外侧距下底1.5cm的点A处有一只蜘蛛.在蜘蛛正对面的圆柱形容器的外侧.距上底1.5cm处的点B处有一只苍蝇.蜘蛛急于捕捉苍蝇充饥.请你帮蜘蛛计算它沿容器侧面爬行的最短距离．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，圆柱形玻璃容器高19cm，底面周长为60cm，在外侧距下底1.5cm的点A处有一只蜘蛛，在蜘蛛正对面的圆柱形容器的外侧，距上底1.5cm处的点B处有一只苍蝇，蜘蛛急于捕捉苍蝇充饥，请你帮蜘蛛计算它沿容器侧面爬行的最短距离．

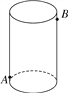
【答案】蜘蛛沿容器侧面爬行的最短距离为34cm.

【解析】试题分析：将圆柱侧面展开成长方形MNQP，过点B作BC⊥MN于点C，连接AB，线段AB的长度即为所求的最短距离,利用勾股定理进行运算即可.

试题解析：如图，将圆柱侧面展开成长方形MNQP，过点B作BC⊥MN于点C，连接AB，

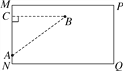
则线段AB的长度即为所求的最短距离．

在Rt△ACB中，AC＝MN－AN－CM＝16cm，

BC是上底面的半圆周的长，即BC＝30cm.

由勾股定理，得AB2＝AC2＋BC2＝162＋302＝1156＝342，

所以AB＝34cm.

故蜘蛛沿容器侧面爬行的最短距离为34cm.

练习册系列答案

成龙计划高效课时学案系列答案

相关题目

（1）如图1，直接写出∠A和∠C之间的数量关系________；

（2）如图2，过点B作BD⊥AM于点D，试说明：∠ABD=∠C；

（3）如图3，在（2）问的条件下，点E在DM上，且BE平分∠DBC，试说明∠ABE=∠AEB．

【题目】已知二次函数y=﹣ x2﹣3x﹣ ，设自变量的值分别为x1 ， x2 ， x3 ，且﹣3＜x1＜x2＜x3 ，则对应的函数值y1 ， y2 ， y3的大小关系是（）
A.y1＞y2＞y3
B.y1＜y2＜y3
C.y2＞y3＞y1
D.y2＜y3＜y1

【题目】杨辉三角是一个由数字排列成等腰三角形数表，一般形式如图所示，其中每一横行都表示（此处，，，，，，）的展开式中的系数，杨辉三角最本质的特征是，它的两条斜边都是由数字组成的，而其余的数则是等于它“肩”上的两个数之和．

上图的构成规律你看懂了吗？

（1）请你直接写出__________________．

杨辉三角还有另一个特征

（2）从第二行到第五行，每一行数字组成的数（如第三行为）都是上一行的数与_____积．

（3）由此你可写出=_________________．

【题目】如图，已知四边形ABCD内接于⊙O，直径AC=6，对角线AC、BD交于E点，且AB=BD，EC=1，则AD的长为（）
A.
B.
C.
D.3

（1）填空：m= ， n=；
（2）若该年级有学生800人，请你估计这个年级最喜爱篮球的学生人数；
（3）在这次调查中随机抽中一名最喜爱足球的学生的概率是多少？

求证：DE∥FC

试题分类