题目内容
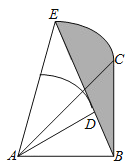
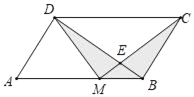
【题目】如图，已知M是平行四边形ABCD中AB边的三等分点，BD与CM交于E，则阴影部分面积与平行四边形面积比为_____．
【答案】7：24
【解析】
利用平行四边形的性质得到AB∥CD，S△BDC=S△ABD，再证明△BME∽△DCE得到
，所以
，
，设BME的面积为S，则S△CDE=9S，S△BCE=3S，从而得到S△BMC=S△DBM=4S，然后计算阴影部分面积与平行四边形面积比．
解：∵四边形ABCD为平行四边形，
∴AB∥CD，S△BDC=S△ABD．
∵M是平行四边形ABCD中AB边的三等分点，
∴CD=AB=3BM．
∵BM∥CD，
∴△BME∽△DCE，
∴
∴，，
设BME的面积为S，则S△CDE=9S，S△BCE=3S，
∴S△BMC=S△DBM=4S，
∴阴影部分面积与平行四边形面积比=（4S+3S）：（9S+3S+9S+3S）=7：24．
故答案为：7：24．
练习册系列答案
相关题目
