题目内容
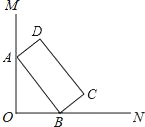
【题目】如图，ABCD绕点A逆时针旋转30°，得到□AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=（ ）
A．155° B．170° C．105° D．145°
【答案】C
【解析】
试题分析:先根据旋转的性质得到AB=AB′，∠BAB′=30°，再根据等腰三角形的性质和三角形内角和定理可得到∠B=∠AB′B=75°，然后根据平行四边形的性质得
AB∥CD，再根据平行线的性质计算得∠C=180°﹣∠B=105°．
解：∵ABCD绕点A逆时针旋转30°，得到□AB′C′D′′，
∴AB=AB′，∠BAB′=30°，
∴∠B=∠AB′B=
（180°﹣30°）=75°，
∵四边形ABCD为平行四边形，
∴AB∥CD，
∴∠B+∠C=180°，
∴∠C=180°﹣75°=105°．
故选C．
练习册系列答案
相关题目
