题目内容
矩形纸片ABCD中,AB=3,AD=4,将纸片折叠,使点B落在边CD上的B’处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为__◆ .

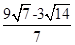
解:根据折叠的性质知:BP=PB′,若点P到CD的距离等于PB,则此距离必与B′P相同,所以该距离必为PB′.延长AE交CD的延长线于F.
由题意知:AB=AB′=3,∠BAE=∠B′AE,
∵Rt△ACB′中,AB′=3,AC= ,
,
∴CB′= ,
,
由于DF∥AB,则∠F=∠BAE,
又∵∠BAE=∠B′AE,
∴∠F=∠B′AE,
∴FB′=AB′=3;
∵PB′⊥CD,AC⊥CD,
∴PB′∥AC,
∴PB′/ AC =FB′/ FC ,
∴PB′ /7 =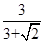 ,
,
解得:PB'=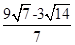
由题意知:AB=AB′=3,∠BAE=∠B′AE,
∵Rt△ACB′中,AB′=3,AC=
 ,
,∴CB′=
 ,
,由于DF∥AB,则∠F=∠BAE,
又∵∠BAE=∠B′AE,
∴∠F=∠B′AE,
∴FB′=AB′=3;
∵PB′⊥CD,AC⊥CD,
∴PB′∥AC,
∴PB′/ AC =FB′/ FC ,
∴PB′ /7 =
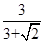 ,
,解得:PB'=
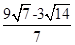

练习册系列答案
相关题目
 中,
中,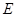 是
是 的中点,将
的中点,将 沿
沿 折叠后得到
折叠后得到 ,且点
,且点 在矩形
在矩形 交
交 于点
于点

 与
与 之长是否相等, 并说明理由.
之长是否相等, 并说明理由. ,求
,求 的值.
的值. ,求
,求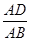 的值.
的值. 滑动到点A为止,同时点F从点B出发,沿图中所示方向按
滑动到点A为止,同时点F从点B出发,沿图中所示方向按 滑动到点B为止,那么在这个过程中,线段QF的中点M所经过的路线长为 ▲ .
滑动到点B为止,那么在这个过程中,线段QF的中点M所经过的路线长为 ▲ .




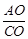 的值为 ( )
的值为 ( )



