题目内容
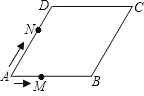
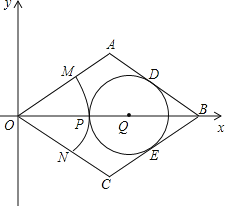
【题目】如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边在直线y=![]() x上,AB边在直线y=-
x上,AB边在直线y=-![]() x+2上.
x+2上.
(1)直接写出:线段OA等于多少,∠AOC等于多少度;
(2)在对角线OB上有一动点P,以O为圆心,OP为半径画弧MN,分别交菱形的边OA、OC于点M、N,作⊙Q与边AB、BC、弧MN都相切,⊙Q分别与边AB、BC相切于点D、E,设⊙Q的半径为r,OP的长为y,求y与r之间的函数关系式,并写出自变量r的取值范围;
(3)若以O为圆心、OA长为半径作扇形OAC,请问在菱形OABC中,在除去扇形OAC后的剩余部分内,是否可以截下一个圆,使得它与扇形OAC刚好围成一个圆锥,若可以,求出这个圆的半径,若不可以,说明理由.
【答案】(1)AO=2,∠AOC=60°;(2)y=2![]() -3r,其中
-3r,其中![]() ;(3)可以,能截下一个圆,使得它与扇形OAC刚好围成一个圆锥.理由见解析.
;(3)可以,能截下一个圆,使得它与扇形OAC刚好围成一个圆锥.理由见解析.
【解析】
(1)令y=-![]() x+2=0,则x=2
x+2=0,则x=2![]() ,即:OB=2
,即:OB=2![]() ,AO=
,AO=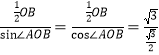 =2,即可求解;
=2,即可求解;
(2)OABC是菱形,故:点Q在OB上,在Rt△QDB中,∠QBD=30°,则:QB=2QD=2r,即y+3r=2![]() ,y=2
,y=2![]() -3r,其中
-3r,其中![]() ;
;
(3)可以.理由:弧AC的长为![]() ,设截下的⊙G符合条件,其半径为R,则2πR=
,设截下的⊙G符合条件,其半径为R,则2πR=![]() ,则R=
,则R=![]() ,即可求解.
,即可求解.
(1)令y=-![]() x+2=0,则x=2
x+2=0,则x=2![]() ,即:OB=2
,即:OB=2![]() ,
,
由直线y=![]() x和AB直线y=-
x和AB直线y=-![]() x+2的表达式知,∠AOB=∠ABO=30°,
x+2的表达式知,∠AOB=∠ABO=30°,
AO=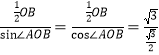 =2,
=2,
∠AOC=2∠AOB=60°,
故:答案为2,60°;
(2)连结QD、QE,则QD⊥AB,QE⊥BC,
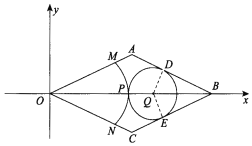
由(1)知:O(0,0),A(![]() ,1),B(2
,1),B(2![]() ,0),C(
,0),C(![]() ,-1),
,-1),
∵QD=QE,∴点Q在∠ABC的平分线上,
又∵OABC是菱形,∴点Q在OB上.
∴⊙Q与弧MN相切于点P,
在Rt△QDB中,∠QBD=30°,
∴QB=2QD=2r,
∴y+3r=2![]() ,
,
y=2![]() -3r,
-3r,
其中![]() .
.
(3)可以,
理由:弧AC的长为![]() .
.
设截下的⊙G符合条件,其半径为R,
则2πR=![]() ,
,
∴R=![]() ,
,
由(2)知,此时OA=y=2,
则⊙Q的半径r=![]() ,
,
∴能截下一个圆,使得它与扇形OAC刚好围成一个圆锥.

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.