题目内容
如图1,在平面直角坐标系中,有一矩形ABCD,其三个顶点的坐标分别为A(2,0)、B(8,0)、C(8,3).将直线l:y=-3x-3以每秒3个单位的速度向右运动,设运动时间为t秒.

(1)当t=_________时,直线l经过点A.(直接填写答案)
(2)设直线l扫过矩形ABCD的面积为S,试求S>0时S与t的函数关系式.
(3)在第一象限有一半径为3、且与两坐标轴恰好都相切的⊙M,在直线l出发的同时,⊙M以每秒2个单位的速度向右运动,如图2所示,则当t为何值时,直线l与⊙M相切?
(1)1;
(2)当1<t≤ 时,S=
时,S=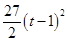 ;
;
当 <t≤3时,S=9t-
<t≤3时,S=9t-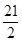 ;
;
当3<t≤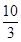 时,S=-
时,S=-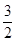 (3t-10)2+18;
(3t-10)2+18;
当t>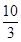 时,S=18;
时,S=18;
(3)t=5-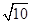 或t=5+
或t=5+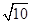 .
.
解析试题分析:(1)y=-3x-3与x轴交点坐标是(-1,0),直线l经过点A(2,0),故向右平移3个单位长度,直线l:y=-3x-3以每秒3个单位的速度向右运动,所以t=1;
(2)求出直线l:y=﹣3x+9t﹣3,再分情况讨论;
(3)分两种情况讨论,借助三角形相似即可.
试题解析:(1)y=-3x-3与x轴交点坐标是(-1,0),直线l经过点A(2,0),故向右平移3个单位长度,直线l:y=-3x-3以每秒3个单位的速度向右运动,所以t=1;
(2)由题意,可知矩形ABCD顶点D的坐标为(2,3).
由一次函数的性质可知,当t由小到大变化时,直线l:y=﹣3(x﹣3t)-3=﹣3x+9t﹣3向右平移,依次扫过矩形ABCD的不同部分.
可得当直线经过A(2,0)时,t=1;当直线经过D(2,3)时,t= ;当直线经过B(8,0)时,t=3;当直线经过C(8,3)时,t=
;当直线经过B(8,0)时,t=3;当直线经过C(8,3)时,t=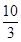 .
.
①当1<t≤ 时, 如图所示.
时, 如图所示. 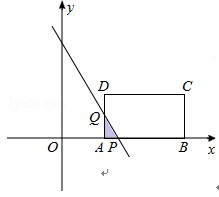
设直线l:y=-3x+9t﹣3与x轴交于点P,与AD交于点Q.
令y=0,可得x=3t﹣1,∴AP=3t﹣3;
令x=2,可得y=9t﹣9,∴AQ=9t﹣9.
∴S=S△APQ=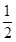 AP•AQ=
AP•AQ=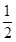 (3t﹣3)( 9t﹣9)=
(3t﹣3)( 9t﹣9)=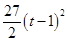 ;
;
②当 <t≤3时,如图所示.
<t≤3时,如图所示. 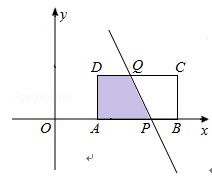
设直线l:y=-3x+9t﹣3与x轴交于点P,与CD交于点Q.
令y=0,可得x=3t﹣1,∴AP=3t﹣3;
令y=3,可得x=3t﹣2,∴DQ=3t﹣4.
S=S梯形APQD=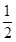 (DQ+AP)•AD=9t-
(DQ+AP)•AD=9t-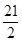 ;
;
③当3<t≤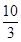 时,如图所示.
时,如图所示. 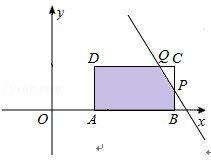
设直线l:y=-3x+9t﹣3与BC交于点P,与CD交于点Q.
令x=8,可得y=9t﹣27,∴BP=9t﹣27,CP=30﹣9t;
令y=3,可得x= 3t﹣2,∴DQ= 3t﹣4,CQ=10﹣3t.
S=S矩形ABCD﹣S△PQC=18﹣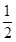 CP•CQ=-
CP•CQ=-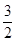 (3t-10)2+18;
(3t-10)2+18;
④当t>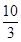 时,S=S矩形ABCD=18.
时,S=S矩形ABCD=18.
综上所述, S与t的函数关系式为: ;
;
(3)若直线l:y=﹣3x+9t﹣3与⊙M相切,如图所示,应有两条符合条件的切线.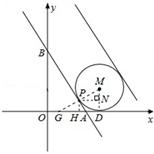
设直线与x轴、y轴交于A、B点,则A(3t﹣1,0)、B(0,9t﹣3),∴OB=3OA.
由题意,可知⊙M与x轴相切,设切点为D,连接MD;
设直线与⊙M的一个切点为P,连接MP并延长交x轴于点G;过P点作PN⊥MD于点N,PH⊥x轴于点H.
易证△PMN∽△BAO,∴PN:MN=OB:OA=3,∴PN=3MN.
在Rt△PMN中,由勾股定理得:PM2=PN2+MN2,解得: MN=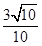 ,PN=
,PN=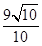 ,
,
∴PH=ND=MD﹣MN=3﹣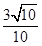 ,OH=OD﹣HD=OD﹣PN=2t+3﹣
,OH=OD﹣HD=OD﹣PN=2t+3﹣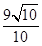 ,
,
∴P(2t+3﹣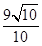 ,3﹣
,3﹣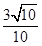 ),代入直线解析式求得:t=5﹣
),代入直线解析式求得:t=5﹣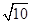 ;
;
同理,当切线位于另外一侧时,可求得:t=5+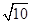 .
.
考点:动点问题.

某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
| | 每件T恤的利润(元) | 销售量(件) |
| 第一个月 | | |
| 清仓时 | | |
 (单位:
(单位: )与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为
)与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为 (单位:
(单位: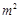 ),其中y2=-2000x+26000(6≤x≤11,x为整数).
),其中y2=-2000x+26000(6≤x≤11,x为整数). 的函数关系式;
的函数关系式; ,于是决定将12月份的销售价格在11月的基础上增加
,于是决定将12月份的销售价格在11月的基础上增加 ,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为
,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为 万元,请根据以上条件求出
万元,请根据以上条件求出 的值为多少?
的值为多少? 中,函数y与自变量x的部分对应值如下表:
中,函数y与自变量x的部分对应值如下表: ?
?  元,出厂价为每件
元,出厂价为每件 元,每月销售量
元,每月销售量 (件)与销售单价
(件)与销售单价 (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:  .
. 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元? (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润? 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?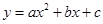 经过点A、B和D(4,
经过点A、B和D(4, ).
).
 时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由. 与y轴交于(0,3),
与y轴交于(0,3),