题目内容
我区某房地产开发公司于2013年5月份完工一商品房小区,6月初开始销售,其中6月的销售单价为0.7万元/m2,7月的销售单价为0.72万元/m2,且每月销售价格 (单位:
(单位: )与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为
)与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为 (单位:
(单位: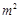 ),其中y2=-2000x+26000(6≤x≤11,x为整数).
),其中y2=-2000x+26000(6≤x≤11,x为整数).
(1)求 与月份
与月份 的函数关系式;
的函数关系式;
(2)6~11月中,哪一个月的销售额最高?最高销售额为多少万元?
(3)2013年11月时,因受某些因素影响,该公司销售部预计12月份的销售面积会在11月销售面积基础上减少 ,于是决定将12月份的销售价格在11月的基础上增加
,于是决定将12月份的销售价格在11月的基础上增加 ,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为
,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为 万元,请根据以上条件求出
万元,请根据以上条件求出 的值为多少?
的值为多少?
(1)y1=0.02x+0.58;(2)6月份的销售额最大为9800万元;(3)3.
解析试题分析:(1)设y1=kx+b,运用待定系数法求解即可.
(2)根据题意表示出月销售额W的表达式,然后根据二次函数的最值可求得答案.
(3)先求出11月的销售面积为及11月份的销售价格,然后根据题意可得出关于a的一元二次方程,解出即可得出答案.
试题解析:(1)设y1=kx+b(k≠0),由题意得: 解得:
解得: 
∴y1=0.02x+0.58.
(2)设第x个月的销售额为W万元,
则W=y1y2=(0.02x+0.58)(-2000x+26000)
=-40x2-640x+15080,
∴对称轴为直线x=-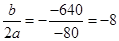 ,
,
∵当6≤x≤11是W随x的增大而减小,
∴当x=6时,
Wmax=-40×62-640×6+15080=9800(6分)
∴6月份的销售额最大为9800万元.
(3)11月的销售面积为:-2000×11+26000=4000(m2)
11月份的销售价格为:0.02×11+0.58=0.8(万元/m2)
由题意得:4000(1-20a%)×0.8(1+a%)+1500+600a=4618.4,
化简得:4a2+5a-51=0,解得:a1=3,a2=? (舍去)
(舍去)
∴a=3.
考点: 1.二次函数的应用;2.一元二次方程的应用;3.待定系数法求一次函数解析式.

 与x轴交于A(1,0)、B(3,0)两点;二次函数
与x轴交于A(1,0)、B(3,0)两点;二次函数 的顶点为P.
的顶点为P. 与抛物线L2交于E,F两点,问线段EF的长度是否发生变化?如果不发生变化,请求出EF的长度;如果发生变化,请说明理由.
与抛物线L2交于E,F两点,问线段EF的长度是否发生变化?如果不发生变化,请求出EF的长度;如果发生变化,请说明理由.


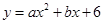 ,求其解析式?
,求其解析式? ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).



