题目内容
抛物线y=- 与y轴交于(0,3),
与y轴交于(0,3),
⑴求m的值;
⑵求抛物线与x轴的交点坐标及顶点坐标;
⑶当x取何值时,抛物线在x轴上方?
⑷当x取何值时,y随x的增大而增大?
(1)m=3;(2)(-1,0),(3,0);(1,4);(3)-1<x<3;(4)x>1.
解析试题分析:(1)直接把点(0,3)代入抛物线解析式求m,确定抛物线解析式,根据解析式确定抛物线的顶点坐标,对称轴,开口方向,与x轴及y轴的交点,画出图象.
(2)、(3)、(4)可以通过(1)的图象及计算得到.
试题解析:(1)由抛物线y=-x2+(m-1)x+m与y轴交于(0,3)得:m=3.
∴抛物线为y=-x2+2x+3=-(x-1)2+4.
列表得:
图象如图:X -1 0 1 2 3 y 0 3 4 3 0 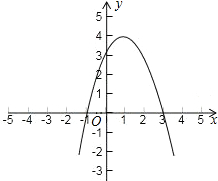
(2)由-x2+2x+3=0,得:x1=-1,x2=3.
∴抛物线与x轴的交点为(-1,0),(3,0).
∵y=-x2+2x+3=-(x-1)2+4
∴抛物线顶点坐标为(1,4).
(3)由图象可知:
当-1<x<3时,抛物线在x轴上方.
(4)由图象可知:当x>1时,y的值随x值的增大而减小.
考点: 1.二次函数的图象;2.二次函数的性质.

练习册系列答案
相关题目
某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x > 40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | |
| 销售玩具获得利润w(元) | |
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
 ,
, .设
.设 米,
米, 米.
米.
 与
与 之间的函数解析式;
之间的函数解析式; ?
?


 ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。

 为对称轴的抛物线
为对称轴的抛物线 与
与 轴交于A、B两点,其中点A的坐标为
轴交于A、B两点,其中点A的坐标为 .
. 、N
、N 在抛物线线上,且
在抛物线线上,且 ,试比较
,试比较 、
、 的大小.
的大小.