��Ŀ����
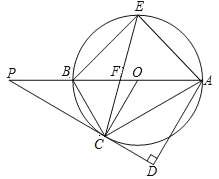
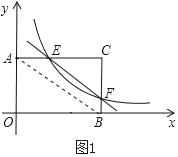
����Ŀ������AOBC�У�OB��8��OA��4���ֱ���OB��OA����ֱ��Ϊx�ᣬy�ᣬ������ͼ1��ʾ��ƽ��ֱ������ϵ��F��BC����һ�����㣨����B��C�غϣ�������F�ķ���������y��![]() ��k��0����ͼ�����AC���ڵ�E��
��k��0����ͼ�����AC���ڵ�E��
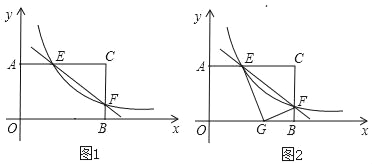
��1������F�˶�����BC���е�ʱ�����E�����ꣻ
��2������EF��AB����֤��EF��AB��
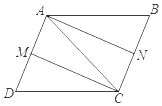
��3����ͼ2������CEF��EF�۵�����Cǡ�����ڱ�OB�ϵĵ�G�������ʱ�����������Ľ���ʽ��
���𰸡���1��E��4��4������2������������3��y��![]()
��������
��1������ȷ����F���꣬�����������������ʽ���ٸ��ݽ���ʽ��õ�E���꼴�ɣ�
��2������AB���ֱ������EFC����ABC������ֵ���ɽ�����⣻
��3���������������жϳ�Rt��MEG��Rt��BGF����ȷ������E��F�������EG��8��![]() ��GF��4��
��GF��4��![]() �����BD������ù��ɶ��������������k���ɵó����ۣ�
�����BD������ù��ɶ��������������k���ɵó����ۣ�
�⣺��1�����ı���OACB�Ǿ��Σ�OB��8��OA��4��
��C��8��4����
�ߵ�F��BC�е㣬
��F��8��2����
�ߵ�F��y��![]() �ϣ�
�ϣ�
��k=16����������������ʽΪy��![]()
�ߵ�E�ڷ���������ͼ���ϣ���E���������Ϊ4��
��4��![]()
��x=4
��E��4��4����
��2������AB�����F��8��a����
��k��8a��
��E��2a��4����
��CF��4��a��EC��8��2a��
��Rt��ECF��tan��EFC��![]() ��2��
��2��
��Rt��ACB��tan��ABC��![]() ��2��
��2��
��tan��EFC��tan��ABC��
���EFC����ABC��
��EF��AB��
��3����ͼ��
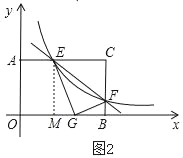
�轫��CEF��EF�۵���Cǡ������OB�ϵ�G�㴦��
���EGF����C��90����EC��EG��CF��GF��
���MGE+��FGB��90����
����E��EM��OB��
���MGE+��MEG��90����
���MEG����FGB��
��Rt��MEG��Rt��BGF��
��![]() ��
��
�ߵ�E��![]() ��4����F��8��
��4����F��8��![]() ����
����
��EC��AC��AE��8��![]() ��CF��BC��BF��4��
��CF��BC��BF��4��![]() ��
��
��EG��EC��8��![]() ��GF��CF��4��
��GF��CF��4��![]() ��
��
��EM��4��
��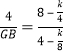 ��
��
��GB��2��
��Rt��GBF��GF2��GB2+BF2��
������4��![]() ��2����2��2+��
��2����2��2+��![]() ��2��
��2��
��k��12��
�෴������������ʽΪy��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�