题目内容
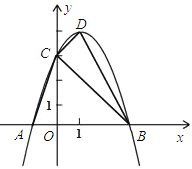
【题目】如图,已知抛物线y=- x2+bx+c与x轴交于点A(-1,0)和B,与y轴交于点C(0,3).
(1)求此抛物线的解析式及点B的坐标;
(2)设抛物线的顶点为D,连接CD、DB、CB、AC.
①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P,使以P、A、C为顶点的三角形与△DCB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由;
【答案】(1)(3,0);(2)①见解析, ② P1(9,0)或P2(0, ![]() )
)
【解析】试题分析:(1)由C(0,3)得出抛物线解析式为y=-x2+bx+3,将点A的横纵坐标代入解析式求出b,令y=0,解出x即可得点B 的坐标;(2)作DE⊥y轴交于点E,不难求出∠ACB=∠DCE=45°, 则∠DCB=∠AOC=90°,由勾股定理求出CD、BC=的长度,不难发现![]() ,即可证明△AOC∽△DCB;②分情况讨论:1.以C为顶点的角是90°时;2.以A为顶点的角是90°时,分别求出点P的坐标即可.
,即可证明△AOC∽△DCB;②分情况讨论:1.以C为顶点的角是90°时;2.以A为顶点的角是90°时,分别求出点P的坐标即可.
试题解析:
解:(1)∵C(0,3),∴抛物线解析式为y=-x2+bx+3,
∵A(-1,0),∴-1-b+3=0,解得b=2.
∴抛物线的解析式为:y=-x2+2x+3,
令y=0,则-x2+2x+3=0,解得:x1=-1,x2=3,
∴点B的坐标是(3,0);
(2)①证明:作DE⊥y轴交于点E,
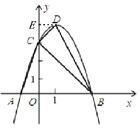
可求得顶点D(1,4),OA=1,OC=OB=3,
∴∠OCB=45°,DE=1,EO=4,
∴EC=1,
∴∠DCE=45°,
故∠DCB=90°=∠AOC,
由勾股定理求得:CD=![]() ,BC=3
,BC=3![]() ,
,
∴![]() ,
,
∴△AOC∽△DCB.
②存在符合条件的点P有两个:P1(9,0)或P2(0, ![]() ).
).
1.以C为顶点的角是90°时,
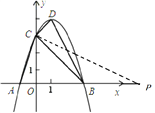
∵∠ACO+∠CAO=90°,∠CPO+∠OCP=90°,
∴∠CPO=∠ACO,
∴∠CPO=∠DBC,
∵∠DCB=∠ACP=90°,
∴△PCA∽△BCD,
∴∠DBC=∠APC,
∴tan∠DBC=tan∠APC,即![]() =
=![]() ,
,
∴OP=9,
∴P(9,0);
2.以A为顶点的角是90°时,
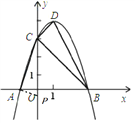
同理可证△AOP∽△BCD,
∴∠DBC=∠PAO,
∴tan∠DBC=tan∠PAO,即![]() =
=![]() ,
,
∴OP=![]() ,
,
∴P(0, ![]() ).
).
综上可得:存在符合条件的点P有两个:P1(9,0)或P2(0, ![]() ).
).