��Ŀ����
����Ŀ����1����֤���عˡ�֤������������λ�߶�����
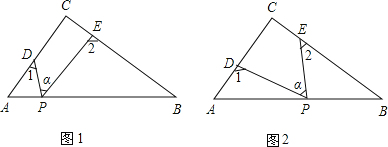
��֪����ͼ1��DE�ǡ�ABC����λ�ߣ�
��֤���� ����
֤�������Ӹ����ߣ���ͼ1���ڡ�ABC�У��ӳ�DE ��D��E�ֱ���AB��AC���е㣩����F��ʹ��EF=DE������CF��
��������֤�����̣�

��2������������
��ͼ2����������ABCD�У�EΪAD���е㣬G��F�ֱ�ΪAB��CD���ϵĵ㣬��AG=2��DF=3����GEF=90�㣬��GF�ij���
��3������չ�о���
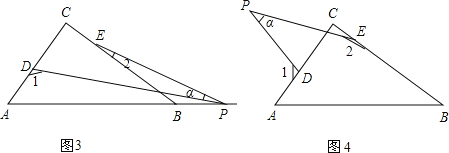
��ͼ3�����ı���ABCD�У���A=105�㣬��D=120�㣬EΪAD���е㣬G��F�ֱ�ΪAB��CD���ϵĵ㣬��AG=![]() ��DF=2����GEF=90�㣬��GF�ij���
��DF=2����GEF=90�㣬��GF�ij���
���𰸡���1��DE��BC��DE=![]() BC,֤��������;��2��5; (3)
BC,֤��������;��2��5; (3) ![]() ��
��
����������1�����������������ε���λ�߶�����д���ɣ����á��߽DZߡ�֤����ADE�͡�CFEȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵá�A=��ECF��ȫ�������ζ�Ӧ����ȿɵ�AD=CF��Ȼ������ı���BCFD��ƽ���ı��Σ�����ƽ���ı��ε�����֤�����ɣ�(2)�ɣ����������ʼ�EΪAD �е�ó���ADE�ա�CFE����ȫ���������Ƴ���EF��ֱƽ��GH���Ӷ����.(3) ����D��AB��ƽ���߽�GE���ӳ����ڵ�H����H��CD�Ĵ��ߣ�����ΪP������HF����֤����AEG�ա�DEH����������ɵõ���HPDΪ����ֱ�������Σ������PF�ij�����Rt��HFP�У������HF��������GF�ij���
��1��DE��BC��DE=![]() BC
BC
֤�����ڡ�ADE�͡�CFE�У� 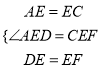 �����ADE�ա�CFE��SAS����
�����ADE�ա�CFE��SAS����
���A=��ECF��AD=CF����CF��AB���֡�AD=BD����CF=BD��
���ı���BCFD��ƽ���ı��Σ���DE��BC��DE=![]() BC��
BC��
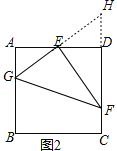
��2����ͼ2���ӳ�GE��FD���ڵ�H��
��EΪAD�е㣬
��EA=ED���ҡ�A=��EDH=90�㣬
�ڡ�AEG�͡�DEH��
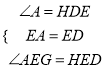 ���AEG�ա�DEH��ASA����
���AEG�ա�DEH��ASA����
��AG=HD=2��EG=EH���ߡ�GEF=90�㣬��EF��ֱƽ��GH��
��GF=HF=DH+DF=2+3=5��
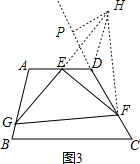
��3����ͼ3������D��AB��ƽ���߽�GE���ӳ����ڵ�H����H��CD�Ĵ��ߣ�����ΪP������HF��
ͬ��1����֪��AEG�ա�DEH��GF=HF�����A=��HDE=105�㣬AG=HD=![]() ��
��
�ߡ�ADC=120�㣬���HDF=360�㩁105�㩁120��=135�㣬
���HDP=45�㣬���PDHΪ����ֱ�������Σ�
��PD=PH=3����PF=PD+DF=3+2=5��
��Rt��HFP�У���HPF=90�㣬HP=3��PF=5��
��HF=![]() ==
==![]() ��GF=
��GF=![]() ��
��
�㾦;���⿼�����ı��ε��ۺ�Ӧ�ã������������ε����ʣ�ȫ�������ε��ж������ʣ����������ε����ʣ����ɶ��������⿼��֪ʶ��϶��ۺ��Խ�ǿ���ѶȽϴ�.