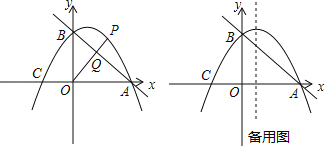
题目内容
【题目】如图,直线l:y=﹣m与y轴交于点A,直线a:y=x+m与y轴交于点B,抛物线y=x2+mx的顶点为C,且与x轴左交点为D(其中m>0).
(1)当AB=12时,在抛物线的对称轴上求一点P使得△BOP的周长最小;
(2)当点C在直线l上方时,求点C到直线l距离的最大值;
(3)若把横坐标、纵坐标都是整数的点称为“整点”.当m=2020时,求出在抛物线和直线a所围成的封闭图形的边界上的“整点”的个数.

【答案】(1)△BOP的周长的最小值为6+6![]() ;(2)当m=2时,点C到直线l距离最大,最大值为1;(3)4042个.
;(2)当m=2时,点C到直线l距离最大,最大值为1;(3)4042个.
【解析】
(1)由已知分别求出![]() ,
,![]() ,
,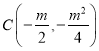 ,
,![]() ;连接BD与对称轴的交点即为P;求出BD的值即可求
;连接BD与对称轴的交点即为P;求出BD的值即可求![]() 的周长的最小值;
的周长的最小值;
(2)点C到直线l距离为![]() ,当
,当![]() 时,该距离有最大值;
时,该距离有最大值;
(3)分别求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 时满足条件的“整数点”的个数,找到规律,由此推理出
时满足条件的“整数点”的个数,找到规律,由此推理出![]() 时,“整数点”的个数.
时,“整数点”的个数.
解:由已知可得A(0,﹣m),B(0,m),
∵y=x2+mx的顶点为C,
∴C(﹣![]() ,﹣
,﹣![]() ),
),
∵y=x2+mx与x轴交点为(0,0),(﹣m,0),
∴D(﹣m,0);
(1)∵AB=12,
∴m=6,
∴D(﹣6,0),B(0,6),
∵抛物线的对称轴为x=﹣![]() ,
,
∴D与O关于x=﹣![]() ,
,
连接BD与对称轴的交点即为P;
∵DP=OP,
∴△BOP的周长=BO+BP+PO=BO+BP+PD=BO+BD;
∵BD=6![]() ,OB=6,
,OB=6,
∴△BOP的周长的最小值为6+6![]() ;
;
(2)∵点C在直线l上方,
∴点C到直线l距离为﹣![]() ﹣(﹣m)=﹣
﹣(﹣m)=﹣![]() +m=﹣
+m=﹣![]() (m﹣2)2+1,
(m﹣2)2+1,
当m=2时,点C到直线l距离最大,最大值为1;
(3)当n=1时,y=x+1与y=x2+x所围成的封闭图形的边界上的“整点”有4个,
当n=2时,y=x+2与y=x2+2x所围成的封闭图形的边界上的“整点”有6个,
当n=3时,y=x+3与y=x2+3x所围成的封闭图形的边界上的“整点”有8个,
当n=4时,y=x+4与y=x2+4x所围成的封闭图形的边界上的“整点”有10个,
……
当n=2020时,y=x+2020与y=x2+2020x所围成的封闭图形的边界上的“整点”有4042个.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案