题目内容
如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点E.若AE=4,CE=8,DE=3,梯形ABCD的高是 ,面积是54.求证:AC⊥BD.
,面积是54.求证:AC⊥BD.
证明见解析.
解析试题分析:由AD∥BC,可证明△EAD∽△ECB,利用相似三角形的性质即可求出BE的长,过D作DF∥AC交BC延长线于F,则四边形ACFD是平行四边形,所以CF=AD,再根据勾股定理的逆定理证明BD⊥DF即可证明AC⊥BD.
试题解析:∵AD∥BC,∴△EAD∽△ECB. ∴AE:CE=DE:BE.
∵AE=4,CE=8,DE=3,∴BE=6.
∵S梯形=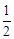 (AD+BC)×
(AD+BC)× =54,∴AD+BC=15.
=54,∴AD+BC=15.
过D作DF∥AC交BC延长线于F,则四边形ACFD是平行四边形,
∴CF="AD." ∴BF=AD+BC=15.
在△BDF中,BD2+DF2=92+122=225,BF2=225,∴BD2+DF2=BF2. ∴BD⊥DF.
∵AC∥DF,∴AC⊥BD.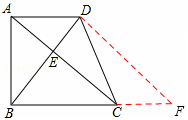
考点:1.梯形的性质;2.相似三角形的判定和性质;3.平行四边形的判定和性质;4.勾股定理的逆定理.

练习册系列答案
相关题目
如图1放置的一个机器零件,若其主(正)视图如图2,则其俯视图是( )
A. | B. | C. | D. |



 ;
;
 ;
;

 是等边三角形,点
是等边三角形,点 、
、 分别在边
分别在边 、
、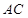 上,
上, .
.
 ∽△
∽△ ;(2)如果
;(2)如果 ,
, ,求
,求 的长.
的长.