Question

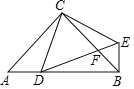
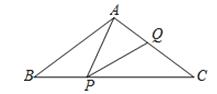
【题目】如图，在△ABC中，已知AB=AC=5cm，BC=8 cm，点P在边BC上沿B到C的方向以每秒1cm的速度运动（不与点B，C重合），点Q在AC上，且满足∠APQ=∠B，设点P运动时间为t秒，当△APQ是等腰三角形时，t=_____．

Answer 1

【答案】3或．

【解析】

分两种情形①如图1中，当PA＝PQ时，作AF⊥BC于F，PE⊥AC于E．②如图2中，当QA＝QP时，作PE⊥AC于E．分别求解即可．

①如图1中，当PA＝PQ时，作AF⊥BC于F，PE⊥AC于E．

∵AB＝AC＝5，AF⊥BC，BC＝8，

∴BF＝CF＝4，∠B＝∠C，

∵∠APC＝∠B＋∠BAP＝∠APQ＋∠QPC，

∵∠APQ＝∠B，

∴∠BAP＝∠QPC，

∴△BAP∽△CPQ，

∴，

∴，

∴CQ＝，

∵PA＝PQ，PE⊥AQ，

∴AE＝EQ＝，

∵cos∠C＝＝，

∴，

解得t＝3或13（舍弃）

②如图2中，当QA＝QP时，作PE⊥AC于E．

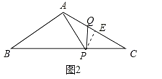
∵QA＝QP，

∴∠QAP＝∠QPA＝∠C，

∴PA＝PC，∵PE⊥AC，

∴AE＝EC＝，

由cos∠C＝，得到，

解得t＝，

综上所述，t＝3秒或秒时，△PQA是等腰三角形．

故答案为3秒或秒．