题目内容
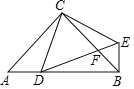
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数;
(3)若AB=4,AD=1,求CD的长.
【答案】(1)见解析;(2)∠BEF=67.5°;(3)![]() .
.
【解析】
(1)由题意可知:CD=CE,∠DCE=90°,由于∠ACB=90°,所以∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,所以∠ACD=∠BCE,从而可证明△ACD≌△BCE(SAS)
(2)由△ACD≌△BCE(SAS)可知:∠A=∠CBE=45°,BE=BF,从而可求出∠BEF的度数;
(3)易证△DBE是直角三角形,由勾股定理可求出DE的长,进而可求出CD的长.
解:(1)证明:由题意可知:CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD与△BCE中,
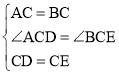 ,
,
∴△ACD≌△BCE(SAS)
(2)∵∠ACB=90°,AC=BC,
∴∠A=45°,
由(1)可知:∠A=∠CBE=45°,
∵AD=BF,
∴BE=BF,
∴∠BEF=67.5°;
(3)∵△ACD≌△BCE,
∴AD=BE=1,∠CBE=∠A=45°,
∵AB=4,
∴DB=3,
∵∠DBE=∠CBA+∠CBE=90°,
∴△DBE是直角三角形,
∴DE=![]() =
=![]() ,
,
∵△CDE是等腰直角三角形,
∴CD=CE=![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目