Question

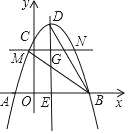
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c经过原点，与x轴交于另一点A，对称轴x=-2交x轴于点C，直线l过点N（0，-2），且与x轴平行，过点P作PM⊥l于点M，△AOB的面积为2．

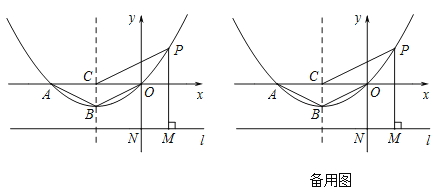
（1）求抛物线的解析式；

（2）当∠MPN=∠BAC时，求P点坐标；

（3）①求证PM=PC；

②若点Q坐标为（0，2），直接写出PQ+PC的最小值．

Answer 1

【答案】（1）；（2）点P坐标为（，）或（，）；（3）①见解析；②PQ+PC的最小值为4.

【解析】

（1）结合经过原点以及顶点和坐标轴进行计算即可；（2）设P点坐标为（x，），将P点在y轴左和右分类讨论解答.（3）①过点P作PD⊥BC于点D，则PD=x+2，DC=，结合（2），在Rt△PCD中运用勾股定理进行计算即可证明；②由①知，PM=PC，当Q、P、M三点共线时， PQ+PC的最小值为PQ+PM的最小值，求出最小值即可.

解：（1）∵抛物线y=ax2+bx+c经过原点，且对称轴为x=-2，

∴c=0，OA=4，又△AOB的面积为2，

∴BC=1，即顶点B的坐标为（-2，-1），

∴，，解得a=，b=1，

∴抛物线的解析式为；

（2）∵BC=1，AC=2，

∴tan∠BAC=，设P点坐标为（x，），如答图1，当点P在y轴右侧，PM=-（-2）=，MN=x，

∴tan∠MPN==，即，此方程无解；

如答图2，当点P在y轴左侧，此时PM=，MN=-x，

∴tan∠MPN==，即，解得，，则，，

∴点P坐标为（，）或（，）；

（3）①如答图3，过点P作PD⊥BC于点D，则PD=x+2，DC=，

由（2）知PM=，在Rt△PCD中，

PC2===PM2，

∴PM=PC；

②由①知，PM=PC，

∴PQ+PC的最小值为PQ+PM的最小值，当Q、P、M三点共线时， PQ+PM=QM,

∵Q（0,2）,

∴QM=QN=4,

∴ PQ+PC的最小值为4．