题目内容
【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC. 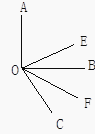
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
【答案】
(1)∵∠AOC=∠AOB+∠BOC,∴∠AOC=90°+60°=150°.∵OE平分∠AOC,∴∠EOC=150°÷2=75°.∵OF平分∠BOC,∴∠COF=60°÷2=30°.∵∠EOC=∠EOF+∠COF,∴∠EOF=75°-30°=45°.
(2)∵OE平分∠AOC,OF平分∠BOC.∴∠COE= ∠AOC,∠COF= ∠BOC∵∠AOB=∠AOC-∠BOC∴∠EOF=∠COE-∠COF= ∠AOC- ∠BOC= (∠AOC-∠BOC)= ∠AOB
(3)∵OE平分∠AOC,OF平分∠BOC,∴∠COE= ∠AOC,∠COF= ∠BOC,
∴∠EOF= ∠AOC- ∠BOC= (∠AOC-∠BOC)= ∠AOB.又∵∠AOB+∠EOF=156°,
∴∠EOF=52°.
【解析】此题难度较大,要通过角度转换.本题考查相交线所形成的角度.
【考点精析】本题主要考查了垂线的性质的相关知识点,需要掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能正确解答此题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目