题目内容
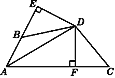
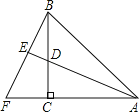
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是( )
A.4 B.3 C.2 D.1
【答案】A.
【解析】
试题分析:①∵BC=AC,∠ACB=90°,∴∠CAB=∠ABC=45°,∵AD平分∠BAC,∴∠BAE=∠EAF=22.5°,∵在Rt△ACD与Rt△BFC中,∠EAF+∠F=90°,∠FBC+∠F=90°,∴∠EAF=∠FBC,∵BC=AC,∠EAF=∠FBC,∠BCF=∠AEF,∴Rt△ADC≌Rt△BFC,∴AD=BF;
故①正确;
②∵①中Rt△ADC≌Rt△BFC,∴CF=CD,故②正确;
③∵①中Rt△ADC≌Rt△BFC,∴CF=CD,AC+CD=AC+CF=AF,∵∠CBF=∠EAF=22.5°,∴在Rt△AEF中,∠F=90°﹣∠EAF=67.5°,∵∠CAB=45°,∴∠ABF=180°﹣∠F﹣∠CAB=180°﹣67.5°﹣45°=67.5°,∴AF=AB,即AC+CD=AB,故③正确;
④由③可知,△ABF是等腰三角形,∵BE⊥AD,∴BE=![]() BF,∵在Rt△BCF中,若BE=CF,则∠CBF=30°,与②中∠CBF=22.5°相矛盾,故BE≠CF,故④错误;
BF,∵在Rt△BCF中,若BE=CF,则∠CBF=30°,与②中∠CBF=22.5°相矛盾,故BE≠CF,故④错误;
⑤由③可知,△ABF是等腰三角形,∵BE⊥AD,∴BF=2BE,故⑤正确.
所以①②③⑤四项正确.
故选A.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目