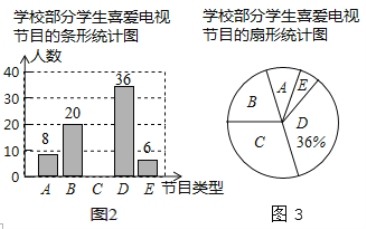
��Ŀ����
����Ŀ��ijˮ����11�·ݹ����ס�������ˮ��������1700Ԫ�����м���ˮ��8Ԫ/ǧ�ˣ�����ˮ��18Ԫ/ǧ�ˣ�12�·ݣ�������ˮ���Ľ����ϵ�Ϊ������ˮ��10Ԫ/ǧ�ˣ�����ˮ��20Ԫ/ǧ�ˣ�
��1�����õ�12�·ݹ���������ˮ����������11�·ݶ���ͬ������֧������300Ԫ����õ�11�·ݹ����ס�������ˮ���ֱ��Ƕ���ǧ�ˣ�
��2����12�·ݽ�������ˮ�������������ٵ�120ǧ�ˣ��蹺������ˮ��aǧ�ˣ���Ҫ֧���Ļ���ΪwԪ����w��a�ĺ�����ϵʽ��
��3���ڣ�2���������£�������ˮ��������90ǧ�ˣ���12�·ݸõ���Ҫ֧��������ˮ���Ļ�������Ӧ�Ƕ���Ԫ��
���𰸡���1���õ�5�·ݹ�������ˮ��100ǧ�ˣ���������ˮ��50ǧ�ˣ���2��w����10a+2400����3��12�·ݸõ���Ҫ֧��������ˮ���Ļ�������Ӧ��1500Ԫ��
��������
(1)��õ�5�·ݽ�����ˮ��xǧ�ˣ���������ˮ��yǧ�ˣ������ܼۣ����ۡ��������ǣ����ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
(2)�蹺������ˮ��aǧ�ˣ���Ҫ֧���Ļ���ΪwԪ��������ˮ��(120-a)ǧ�ˣ������ܼۣ����ۡ��������������ɵó�w����a�ĺ�����ϵʽ��
(3)���ݼ���ˮ��������90ǧ�ˣ��ɵó�a��ȡֵ���̣�������һ�κ��������ʼ��ɽ����ֵ����.
�⣺��1����õ�11�·ݹ�������ˮ��xǧ�ˣ���������ˮ��yǧ�ˣ�
��������ã�![]() ��
��
���![]() ��
��
�𣺸õ�5�·ݹ�������ˮ��100ǧ�ˣ���������ˮ��50ǧ�ˣ�
��2���蹺������ˮ��aǧ�ˣ���Ҫ֧���Ļ���ΪwԪ��������ˮ����120��a��ǧ�ˣ�
��������ã�w��10a+20��120��a������10a+2400��
��3����������ã�a��90���ɣ�2���ã�w����10a+2400��
�ߩ�10��0��w��a���������С��
��a��90ʱ��w����Сֵw��С����10��90+2400��1500��Ԫ����
��12�·ݸõ���Ҫ֧��������ˮ���Ļ�������Ӧ��1500Ԫ��