题目内容
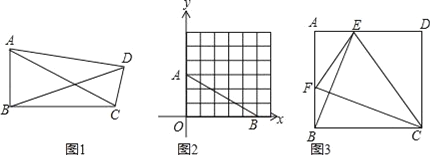
【题目】如图,在长方形ABCD中,O为平面直角坐标系的原点,点的坐标分别为A(a,2)、B(a,-1),D(b,2).且a、b满足![]() .点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
.点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
(1)点C的坐标为_______________
(2)当点P移动在线段BC上时,求三角形ACP的面积(用含t的代数式表示)
(3)在移动过程中,当三角形ACP的面积是5时,直接写出点P移动的时间为几秒

【答案】(1)![]() ;(2)
;(2)![]() ;(3)当三角形ACP的面积是5时,
;(3)当三角形ACP的面积是5时,![]() 、
、![]() 、
、![]() .
.
【解析】
(1)根据![]() 可得到
可得到![]() ,
,![]() ,由矩形的性质可得C点的横坐标与D点的相等,纵坐标与B点相同,即可得到结论;
,由矩形的性质可得C点的横坐标与D点的相等,纵坐标与B点相同,即可得到结论;
(2)因为点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,且当点P移动在线段BC上时,可得BP=t,根据三角形面积公式即可得到结果;
(3)分类讨论,当P在AB上运动和BC上运动进行讨论;
(1)根据![]() 可得:
可得:
![]() 和
和![]() ,
,
解得![]() ,
,![]() ,
,
∴A(2,2)、B(2,-1),D(-4,2),
∵四边形ABCD是矩形,
∴C的横坐标坐标-4,纵坐标为-1,
∴![]() .
.
(2)由题可知BP=t,
由(1)可知,AB=3,BC=6,且点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,
∴当t=3时,P点运动到点B,当t=9时,点P运动到C处,
根据图形可得△ACP的面积=![]() ,
,
∵BP=t-3,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故![]() .
.
(3)当点P在AB边上运动时,
![]() ,
,
当角形ACP的面积是5时,可得![]() ,
,
解得![]() ;
;
当点P在AB边上运动时,
由(1)得![]() ,
,
当角形ACP的面积是5时,可得![]() ,
,
解得:![]() ,
,
当点P在CD上运动时,![]() ,
,
![]()
当角形ACP的面积是5时,可得![]() ,
,
解得:![]() ;
;
当点P在DA上运动时,![]() ,
,
∴DP=t-12,
∴AP=18-(t-12)=30-t,
![]() ,
,
当角形ACP的面积是5时,可得![]() ,
,
解得:![]() (舍去);
(舍去);
故当三角形ACP的面积是5时,![]() 、
、![]() 、
、![]() .
.