题目内容
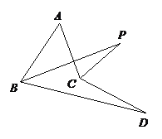
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点是法国数学家和教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=。
【答案】![]()
【解析】解 :如图,在等腰直角三角形△DEF中,∠EDF=90,DE=DF,∠1=∠2=∠3, 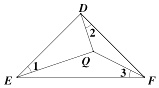
∴∠1+∠QEF=∠3+∠DFQ=45,
∴∠QEF=∠DFQ;sin45°=DF∶EF=1∶![]()
又∵∠2=∠3,
∴△DQF∽△FQE,
∴DQ∶FQ=FQ∶QE=DF∶EF=1∶![]() ,
,
∵DQ=1,
∴FQ=![]() ,EQ=2,
,EQ=2,
∴EQ+FQ=2+![]() ,
,
由等腰直角三角形的性质得出∠1+∠QEF=∠3+∠DFQ=45,进而得出∠QEF=∠DFQ;sin45°=DF∶EF=1∶![]() ,然后判断出△DQF∽△FQE,根据相似三角形对应边成比例得出DQ∶FQ=FQ∶QE=DF∶EF=1∶
,然后判断出△DQF∽△FQE,根据相似三角形对应边成比例得出DQ∶FQ=FQ∶QE=DF∶EF=1∶![]() ,进而求出FQ=
,进而求出FQ=![]() ,EQ=2,从而得出答案。
,EQ=2,从而得出答案。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目