Question

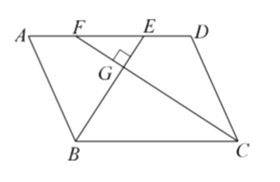
【题目】如图，在四边形中，的平分线交于点的平分线交于点，交于点，且．

（1）求证：四边形是平行四边形；

（2）若，求线段的长．

Answer 1

【答案】（1）见详解；（2）3．

【解析】

（1）证出∠GBC＋∠GCB＝90°，由角平分线的定义得出∠ABC＝2∠GBC，∠BCD＝2∠DCF，得出∠ABC＋∠BCD＝180°，证出AB∥CD，即可得出结论；

（2）由平行四边形的性质得出AD∥BC，DC＝AB＝，AD＝BC＝6，由平行线的性质和角平分线定义证出∠AEB＝∠ABE，得出AE＝AB＝，同理：DF＝DC，得出AE＝DF，AF＝DE，证出2AB＝AD＋EF，即可得出结果．

（1）证明：∵BE⊥CF，

∴∠BGF＝90°，

∴∠GBC＋∠GCB＝90°，

∵∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F，

∴∠ABC＝2∠GBC，∠BCD＝2∠DCF，

∴∠ABC＋∠BCD＝180°，

∴AB∥CD，

∵AB＝CD，

∴四边形ABCD是平行四边形；

（2）解：∵四边形ABCD是平行四边形，

∴AD∥BC，DC＝AB＝，AD＝BC＝6，

∴∠AEB＝∠CBE，

∵∠ABC的平分线交AD于点E，

∴∠ABE＝∠CBE，

∴∠AEB＝∠ABE，

∴AE＝AB＝，

同理：DF＝DC，

∴AE＝DF，

∴AF＝DE，

∵AE＋DF＝AD＋EF，

∴2AB＝AD＋EF，

∴EF＝2ABAD＝96＝3．