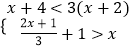题目内容
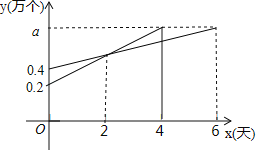
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图)，此图揭示了(a＋b)n(n为非负整数)展开式的项数及各项系数的有关规律．例如：(a＋b)0＝1，它只有一项，系数为1；(a＋b)1＝a＋b，它有两项，系数分别为1，1，系数和为2；(a＋b)2＝a2＋2ab＋b2，它有三项，系数分别为1，2，1，系数和为4；(a＋b)3＝a3＋3a2b＋3ab2＋b3，它有四项，系数分别为1，3，3，1，系数和为8……
根据以上规律，解答下列问题：
(1)(a＋b)4的展开式共有多少项，系数分别为多少；
(2)写出(a＋b)5的展开式；
(3)(a＋b)n的展开式共有多少项，系数和为多少．
【答案】(1)5； 1，4，6，4，1；(2)a5＋5a4b＋10a3b2＋10a2b3＋5ab4＋b5；(3)(n＋1)； 2n.
【解析】
（1）本题通过阅读理解寻找规律，观察可得（a+b）n（n为非负整数）展开式的各项系数的规律：首尾两项系数都是1，中间各项系数等于（a+b）n-1相邻两项的系数和．因此可得（a+b）4的各项系数分别为1、（1+3）、（3+3）、（3+1）、1即可；
（2）由（1）得出的规律，即可得出结果；
（3）根据题意得出（a+b）n展开式共有（n+1）项，当a=b=1时，（a+b）n=2n即可．
解：（1）根据题意知，（a+b）4的展开后，共有5项，
各项系数分别为1、（1+3）、（3+3）、（3+1）、1，
即：1、4、6、4、1；
（2）根据题意得：（a+b）5的展开式为a5+5a4b+10a3b2+10a2b3+5ab4+b5．
（3）根据题意得：(a＋b)n的展开式共有（n+1）项
当a=b=1时，（a+b）n=2n．
即：(a＋b)n的展开式系数和为2n．
