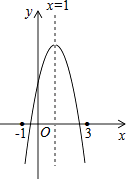Question

【题目】如图，抛物线y=﹣ x2+bx+c与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．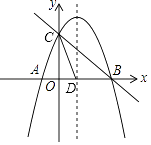

（1）求抛物线的解析式
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，请直接写出P点的坐标；如果不存在，请说明理由．
（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，△CBF的面积最大？请求出△CBF的最大面积及此时E点的坐标．

Answer 1

【答案】
（1）

解：∵A（﹣1，0），C（0，2）在抛物线y= x2+bx+c上，

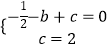∴ ，解得 ，

∴抛物线解析式为y=﹣ x2+ x+2；

（2）

解：∵y=﹣ x2+ x+2=﹣ （x﹣ ）2+ ，

∴抛物线对称轴为直线x= ，

∴D（ ，0），且C（0，2），

∴CD= = ，

∵点P在对称轴上，

∴可设P（ ，t），

∴PD=|t|，PC= ，

当PD=CD时，则有|t|= ，解得t=± ，此时P点坐标为（ ， ）或（ ，﹣ ）；

当PC=CD时，则有 = ，解得t=0（与D重合，舍去）或t=4，此时P点坐标为（ ，4）；

综上可知存在满足条件的点P，其坐标为（ ， ）或（ ，﹣ ）或（ ，4）；

（3）

解：当y=0时，即﹣ x2+ x+2=0，解得x=﹣1或x=4，

∴A（﹣1，0），B（4，0），

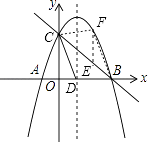
设直线BC解析式为y=kx+s，由题意可得 ，解得 ，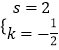

∴直线BC解析式为y=﹣ x+2，

∵点E是线段BC上的一个动点，

∴可设E（m，﹣ m+2），则F（m，﹣ m2+ m+2），

∴EF=﹣ m2+ m+2﹣（﹣ m+2）=﹣ m2+2m=﹣ （m﹣2）2+2，

∴S△CBF= ×4EF=2[=﹣ （m﹣2）2+2]=﹣（m﹣2）2+4，

∵﹣1＜0，

∴当m=2时，S△CBF有最大值，最大值为4，

此时﹣ x+2=1，

∴E（2，1），即E为BC的中点，

∴当E运动到BC的中点时，△CBF的面积最大，最大面积为4，此时E点坐标为（2，1）．

【解析】（1）由A、C的坐标，利用待定系数法可求得抛物线的解析式；（2）可设出P点坐标，则可表示出PC、PD和CD的长，分PD=CD、PC=CD两种情况分别得到关于P点坐标的方程，可求得P点坐标；（3）由B、C的坐标可求得直线BC的解析式，可设出E点坐标，则可表示出F点的坐标，从而可表示出EF的长，可表示出△CBF的面积，再利用二次函数的性质可求得其最大值及此时点E的坐标．