Question

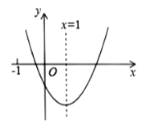
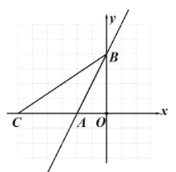
【题目】二次函数（）的图象如图所示，对称轴为，给出下列结论：①； ②当时，；③；④，其中正确的结论有__________．

Answer 1

【答案】①③④

【解析】

根据二次函数图象的开口向上，可得a＞0，根据图象与y轴的交点在y轴的负半轴上，可得c＜0，根据图象的对称轴是直线x=1，结合a＞0可得b＜0，进而可得①正确；再根据当x＞2时，y有小于0的情况，可判断②错误；因为x=－1时，y＞0，∴＞0，再结合对称轴可得2a+b=0，进一步可得，由此判断③正确；最后由2a+b=0，a＞0，可得，所以④正确；到此可得结果.

解：∵二次函数的图象开口向上，∴a＞0，

∵二次函数的图象与y轴的交点在y轴的负半轴上，∴c＜0，

∵二次函数图象的对称轴是直线x=1，

∴，∴2a+b=0，b＜0.

∴；故①正确；

由二次函数的图象可知，抛物线与x轴的右交点的横坐标应大于2小于3，

∴当x＞2时，y有小于0的情况，故②错误；

∵当x=－1时，y＞0，

∴＞0，

把代入得：，故③正确；

前面已得2a+b=0，又∵a＞0，∴，故④正确；

故答案为：①③④.