题目内容
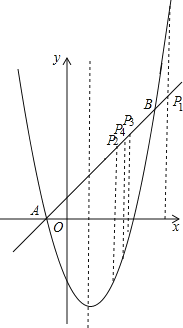
【题目】如图，对称轴为x=1的抛物线经过A（﹣1，0），B（4，5）两点．
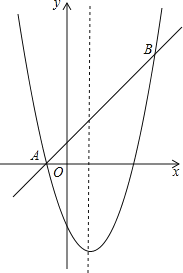
（1）求抛物线的解析式；
（2）P为直线AB上的动点，过点P作x轴的垂线交抛物线于点Q．
①当PQ=6时，求点P的坐标；
②是否存在点P，使以A、P、Q为顶点的三角形为等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．
【答案】（1）y=x2﹣2x﹣3；（2）①当PQ=6时，点P的坐标（1，2），（2，3），（﹣2，﹣1），（5，6）；②存在点P，使以A、P、Q为顶点的三角形为等腰三角形，点P的坐标为P（4+
，5+）或（4﹣，5﹣）或（4，5）或（3.4）．
【解析】
试题分析：（1）根据题意确定抛物线与x轴的另一个交点，然后根据待定系数法即可求得；
（2）①先求得直线AB的解析式，设P（m，m+1），Q（m，m2﹣2m﹣3），则PQ=|m+1﹣m2+2m+3|=6，然后分m2﹣3m﹣4=﹣6或m2﹣3m﹣4=6两种情况求得m的值，从而求得P点的坐标；
②由勾股定理，得PA2=（m+1）2+（m+1）2；PQ2=[m+1﹣（m2﹣2m﹣3）]2，AQ2=（m+1）2+（m2﹣2m﹣3）2．然后分PA=PQ、PA=AQ、AQ=AP三种情况列出关于m的方程，解方程求得m的值，即可求得P点的坐标．
解：（1）对称轴为x=1的抛物线经过A（﹣1，0），得C（3，0），
设抛物线的解析式为y=ax2+bx+c，将A、B、C点坐标代入，得
，
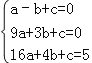解得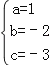
，
设抛物线的解析式为y=x2﹣2x﹣3；
（2）①直线AB的解析式为y=x+1，设P（m，m+1），Q（m，m2﹣2m﹣3），
PQ=|m+1﹣m2+2m+3|=6，
当m2﹣3m﹣4=﹣6，
解得m=1，m=2，
∴P（1，2）或（2，3）；
当m2﹣3m﹣4=6，解得m=﹣2，m=5，
∴P（﹣2，﹣1）或（5，6）；
综上所述：当PQ=6时，点P的坐标（1，2），（2，3），（﹣2，﹣1），（5，6）；
（3）∵A（﹣1，0），P（m，m+1），Q（m，m2﹣2m﹣3），由勾股定理，得
PA2=（m+1）2+（m+1）2；PQ2=[m+1﹣（m2﹣2m﹣3）]2，AQ2=（m+1）2+（m2﹣2m﹣3）2．
①当PA=PQ时，（m+1）2+（m+1）2=[m+1﹣（m2﹣2m﹣3）]2，化简，得（m+1）2[（m﹣4）2﹣2]=0．
于是，得（m﹣4）2﹣2=0，m+1=0．
解得m1=4+
，m2=4﹣，m3=﹣1，
∵当m=﹣1时，P点与A点重合，
∴P1（4+，5+），P2（4﹣，5﹣）；
②当PA=AQ时，（m+1）2+（m+1）2=（m+1）2+（m2﹣2m﹣3）2，化简，得（m+1）2（m﹣3﹣1）2=0，
于是，得（m﹣4）2=0，解得m4=4，m5=﹣1，
∴P3（4，5）；
③当AQ=AP时，（m+1）2+（m2﹣2m﹣3）2=[m+1﹣（m2﹣2m﹣3）]2，化简，得（m+1）2[（m﹣4）2﹣2]=0．
于是，得（m2﹣2m﹣3）2=0．m+1=0，
解得m6=3，m7=﹣1，
∴P（3，4）；
综上，存在点P，使以A、P、Q为顶点的三角形为等腰三角形，点P的坐标为P（4+，5+）或（4﹣，5﹣）或（4，5）或（3.4）．
