��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��0��1����D��-2��0������ֱ��AD�����߶�ADΪһ��������������ABCD��
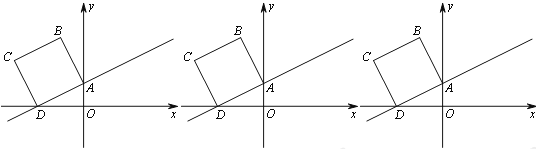
��1����գ���B������Ϊ________����C������Ϊ_________��
��2������������ÿ��![]() ����λ���ȵ��ٶ�������DA����ƽ�ƣ�ֱ�������εĶ���C����y����ʱֹͣ�˶������˶������У�������������y���Ҳಿ�ֵ����ΪS����S����ƽ��ʱ��t�������ĺ�����ϵʽ����д����Ӧ���Ա���t��ȡֵ��Χ��
����λ���ȵ��ٶ�������DA����ƽ�ƣ�ֱ�������εĶ���C����y����ʱֹͣ�˶������˶������У�������������y���Ҳಿ�ֵ����ΪS����S����ƽ��ʱ��t�������ĺ�����ϵʽ����д����Ӧ���Ա���t��ȡֵ��Χ��
���𰸡���1������1��3������2��S= .
.
��������
������������⿼���������ε����ʡ�ȫ�������ε��ж������ʡ�һԪһ�β���ʽ��Ӧ�á������ε������ʽ�Լ�ֱ�����ε������ʽ������Ĺؼ�����1����ȫ�������ε������ҳ���ABB���CC��D���ߵij��ȣ���2����һԪһ�β���ʽ�ҳ���ͬ�����t��ȡֵ��Χ�����������е��⣬��1���ѶȲ�������������⣬���Բ���ȥ֤������ȫ��ʡȥ����ʱ�䣻��2���ѶȲ����ǹ��̷�������������в����õ��˽�һԪһ�β���ʽ��x��ȡֵ��Χ�����õ��������Ρ�ֱ�����ε������ʽ�����ڽ����������Ŀʱ��ϸ�Ĺ۲�ͼ�Σ�ͨ��ͼ�εı仯�����ǹؼ�.
��1������B��BB����y���ڵ�B�䣬����C��CC����x���ڵ�C�䣬��ȫ�������ε����ʿ�֪AB��=CC��=DO��BB��=DC��=AO����ϸ��ߵĹ�ϵ�����ҳ�B��C������ꣻ
��2����ͼ�εı仯�ֳ������֣�����ʱ��t��ʾ��ֱ����������ֱ�DZ߳��ȣ����������������ʽ���ɵó����ۣ�����ʱ��t��ʾ��ֱ�������ϡ��µ���ߵij��ȣ��������ε������ʽ���ɵó����ۣ����������ε������ȥʣ��ֱ�������ε�������ɵó�����.
�����������1������1��3����
��2����0��t��![]() ʱ��S=5t2��
ʱ��S=5t2��
��![]() ��t��1ʱ��S=5t-
��t��1ʱ��S=5t-![]() ��
��
��1��t��![]() ʱ��S=5t2+15t-
ʱ��S=5t2+15t-![]() .
.
���ϣ�S= .
.



