题目内容
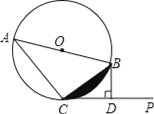
【题目】如图,已知△ABC中,AD是高,AE是角平分线.
(1)若∠B=20°,∠C=60°,求∠EAD度数;
(2)若∠B=α,∠C=β(β>a),求∠EAD.(用α、β的代数式表示)
【答案】
(1)
解答:∵∠B=20°,∠C=60°,
∴∠BAC=180°-20°-60°=100°,
∵AE是角平分线,
∴∠EAC=50°,
∵AD是高,
∴∠ADC=90°,
∴∠DAC=30°,
∴∠EAD=∠EAC-∠DAC=50°-30°=20°;
(2)
∵∠B=α,∠C=β,
∴∠BAC=180°-α-β,
∵AE是角平分线,
∴∠EAC=90°- ![]() α-
α- ![]() β,
β,
∵AD是高,
∴∠ADC=90°,
∴∠DAC=90°-β,
∴∠EAD=∠EAC-∠DAC=(90°- ![]() α-
α- ![]() β)-(90°-β)=
β)-(90°-β)= ![]() (β-α).
(β-α).
【解析】此题考查了三角形内角和定理和三角形的角平分线、高、中线,解题的关键是根据三角形的内角和是180°,分别求出各个角的度数.

练习册系列答案
相关题目