题目内容
一长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD边上(如图).
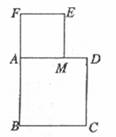
(1)求AM、MD的长;
(2)你能说明点M是线段AD的黄金分割点吗?
解:(1)AM=![]() 一l MD=3一
一l MD=3一![]()
(2)∵AM=![]() 一l,MD=3一
一l,MD=3一![]() ,AD=2
,AD=2
∴MD?AD=(3一![]() )×2= 6―2
)×2= 6―2![]()
AM![]() = (
= (![]() 一l)
一l)![]() =6―2
=6―2![]()
∴AM![]() = MD?AD
= MD?AD
则点M是线段AD的黄金分割点

练习册系列答案
相关题目
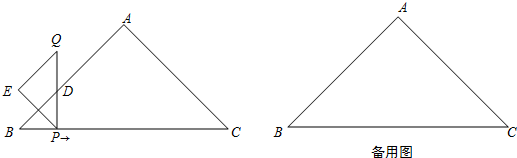

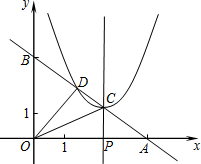 如图,直线y=-
如图,直线y=-