��Ŀ����
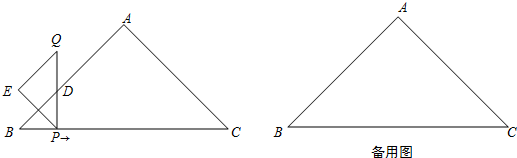
��ͼ����Rt��ABC�У�AB=AC=4
��һ����P�ӵ�B��������BC������ÿ��1����λ���ȵ��ٶ������˶��������C��ֹͣ���������˶������У�����P��PD��BC��Rt��ABC��ֱ�DZ��ཻ�ڵ�D���ӳ�PD����Q��ʹ��PD=QD����PQΪб����PQ���������ֱ��������PQE�����˶�ʱ��Ϊt�루t��0����
��1���������˶������У����ABC���PQE�ص����ֵ����ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ�Լ���Ӧ���Ա���t��ȡֵ��Χ��
��2������D���߶�AB��ʱ������AQ��AP���Ƿ����������t��ʹ�á�APQ��Ϊ���������Σ������ڣ������Ӧ��t��ֵ���������ڣ���˵�����ɣ�
��3����t=4��ʱ����PQΪб����PQ�Ҳ�������ֱ��������PQF�����ı���PEQF�Ƶ�P��ת��PE���߶�AB�ཻ�ڵ�M��PF���߶�AC�ཻ�ڵ�N�����ж�����һ��ת�����У��ı���PMAN������Ƿ����仯���������仯������ı���PMAN�����y��PM�ij�x֮��ĺ�����ϵʽ�Լ���Ӧ���Ա���x��ȡֵ��Χ�����������仯������˶�ֵ��
| 2 |
��1���������˶������У����ABC���PQE�ص����ֵ����ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ�Լ���Ӧ���Ա���t��ȡֵ��Χ��
��2������D���߶�AB��ʱ������AQ��AP���Ƿ����������t��ʹ�á�APQ��Ϊ���������Σ������ڣ������Ӧ��t��ֵ���������ڣ���˵�����ɣ�
��3����t=4��ʱ����PQΪб����PQ�Ҳ�������ֱ��������PQF�����ı���PEQF�Ƶ�P��ת��PE���߶�AB�ཻ�ڵ�M��PF���߶�AC�ཻ�ڵ�N�����ж�����һ��ת�����У��ı���PMAN������Ƿ����仯���������仯������ı���PMAN�����y��PM�ij�x֮��ĺ�����ϵʽ�Լ���Ӧ���Ա���x��ȡֵ��Χ�����������仯������˶�ֵ��

��������1����PQ��Aʱ���t=4����E��AB��ʱ���t=
����P��C��ʱt=8������Ϊ������������������������ʽ�����0��t��4ʱ��S=
t2����4��t��
ʱ��S=-
t2+8t-16����
��t��8ʱ��S=
t2-12t+48��
��2�����ڣ�����D���߶�AB��ʱ�����QD=PD=t��PD=2t������A��AH��BC�ڵ�H��PH=BH-BP=4-t����Rt��APH�����AP=
=
����������AP=PQ������
=2t����������AQ=PQ������Q��QG��AP�ڵ�G�����ݡ�PGQ�ס�AHP���PG=
����AQ=PQ���ó�
=
����������AP=AQ������A��AT��PQ�ڵ�T���ó�4=
��2t��������̵Ľ⼴�ɣ�
��3���ı���PMAN������������仯������AP����ʱt=4�룬���S�ı���PMAN=S��APM+S��APN=S��CPN+S��APN=S��ACP=
��CP��AP=8��
| 16 |
| 3 |
| 1 |
| 4 |
| 16 |
| 3 |
| 3 |
| 4 |
| 16 |
| 3 |
| 3 |
| 4 |
��2�����ڣ�����D���߶�AB��ʱ�����QD=PD=t��PD=2t������A��AH��BC�ڵ�H��PH=BH-BP=4-t����Rt��APH�����AP=
| AH2+PH2 |
| t2-8t+32 |
| t2-8t+32 |
| 8t | ||
|
| 8t | ||
|
| 1 |
| 2 |
| t2-8t+32 |
| 1 |
| 2 |
��3���ı���PMAN������������仯������AP����ʱt=4�룬���S�ı���PMAN=S��APM+S��APN=S��CPN+S��APN=S��ACP=
| 1 |
| 2 |
����⣺��1����0��t��4ʱ��S=
t2��
��4��t��
ʱ��S=-
t2+8t-16��
��
��t��8ʱ��S=
t2-12t+48��
��2�����ڣ��������£�
����D���߶�AB��ʱ��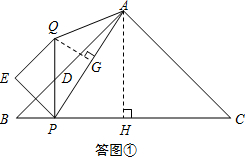
��AB=AC��
���B=��C=
��180��-��BAC��=45�㣮
��PD��BC��
���BPD=90�㣬
���BDP=45�㣬
��PD=BP=t��
��QD=PD=t��
��PQ=QD+PD=2t��
����A��AH��BC�ڵ�H��
��AB=AC��
��BH=CH=
BC=4��AH=BH=4��
��PH=BH-BP=4-t��
��Rt��APH��AP=
=
��
��������AP=PQ������
=2t��
��ã�t1=
��t2=
���������⣬��ȥ����
��������AQ=PQ������Q��QG��AP�ڵ�G����ͼ��1����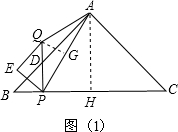
�ߡ�BPQ=��BHA=90�㣬
��PQ��AH��
���APQ=��PAH��
��QG��AP��
���PGQ=90�㣬
���PGQ=��AHP=90�㣬
���PGQ�ס�AHP��
��
=
����
=
��
��PG=
��
��AQ=PQ������QG��AP������AG=PG����PG=
AP��
��
=
��
��ã�t1=12-4
��t2=12+4
���������⣬��ȥ����
��������AP=AQ������A��AT��PQ�ڵ�T����ͼ��2����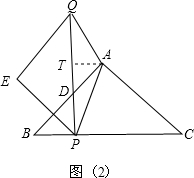
��֪�ı���AHPT�Ǿ��Σ���PT=AH=4��
��AP=AQ������AT��PQ������QT=PT����PT=
PQ��
��4=
��2t�����t=4��
��t=4ʱ��A��P��Q���㹲�ߣ���APQ�����ڣ���t=4��ȥ��
��������������������t��ʹ�á�APQ��Ϊ���������Σ���t1=
���t2=��12-4
���룻
��3���ı���PMAN������������仯���������£�
�ߵ���ֱ��������PQE��
���EPQ=45�㣬
�ߵ���ֱ��������PQF��
���FPQ=45�㣮
���EPF=��EPQ+��FPQ=45��+45��=90�㣬
����AP����ͼ��3����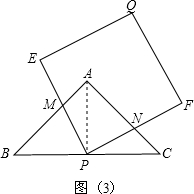
�ߴ�ʱt=4�룬
��BP=4��1=4=
BC��
���PΪBC���е㣮
�ߡ�ABC�ǵ���ֱ�������Σ�
��AP��BC��AP=
BC=CP=BP=4����BAP=��CAP=
��BAC=45�㣬
���APC=90�㣬��C=45�㣬
���C=��BAP=45�㣬
�ߡ�APC=��CPN+��APN=90�㣬
��EPF=��APM+��APN=90�㣬
���CPN=��APM��
���CPN�ա�APM��
��S��CPN=S��APM��
��S�ı���PMAN=S��APM+S��APN=S��CPN+S��APN=S��ACP=
��CP��AP=
��4��4=8��
���ı���PMAN������������仯���˶�ֵΪ8��
| 1 |
| 4 |
��4��t��
| 16 |
| 3 |
| 3 |
| 4 |
��
| 16 |
| 3 |
| 3 |
| 4 |
��2�����ڣ��������£�
����D���߶�AB��ʱ��

��AB=AC��
���B=��C=
| 1 |
| 2 |
��PD��BC��
���BPD=90�㣬
���BDP=45�㣬
��PD=BP=t��
��QD=PD=t��
��PQ=QD+PD=2t��
����A��AH��BC�ڵ�H��
��AB=AC��
��BH=CH=
| 1 |
| 2 |
��PH=BH-BP=4-t��
��Rt��APH��AP=
| AH2+PH2 |
| t2-8t+32 |
��������AP=PQ������
| t2-8t+32 |
��ã�t1=
4
| ||
| 3 |
-4
| ||
| 3 |
��������AQ=PQ������Q��QG��AP�ڵ�G����ͼ��1����

�ߡ�BPQ=��BHA=90�㣬
��PQ��AH��
���APQ=��PAH��
��QG��AP��
���PGQ=90�㣬
���PGQ=��AHP=90�㣬
���PGQ�ס�AHP��
��
| PG |
| AH |
| PQ |
| AP |
| PG |
| 4 |
| 2t | ||
|
��PG=
| 8t | ||
|
��AQ=PQ������QG��AP������AG=PG����PG=
| 1 |
| 2 |
��
| 8t | ||
|
| 1 |
| 2 |
| t2-8t+32 |
��ã�t1=12-4
| 7 |
| 7 |
��������AP=AQ������A��AT��PQ�ڵ�T����ͼ��2����

��֪�ı���AHPT�Ǿ��Σ���PT=AH=4��
��AP=AQ������AT��PQ������QT=PT����PT=
| 1 |
| 2 |
��4=
| 1 |
| 2 |
��t=4ʱ��A��P��Q���㹲�ߣ���APQ�����ڣ���t=4��ȥ��
��������������������t��ʹ�á�APQ��Ϊ���������Σ���t1=
4
| ||
| 3 |
| 7 |
��3���ı���PMAN������������仯���������£�
�ߵ���ֱ��������PQE��
���EPQ=45�㣬
�ߵ���ֱ��������PQF��
���FPQ=45�㣮
���EPF=��EPQ+��FPQ=45��+45��=90�㣬
����AP����ͼ��3����

�ߴ�ʱt=4�룬
��BP=4��1=4=
| 1 |
| 2 |
���PΪBC���е㣮
�ߡ�ABC�ǵ���ֱ�������Σ�
��AP��BC��AP=
| 1 |
| 2 |
| 1 |
| 2 |
���APC=90�㣬��C=45�㣬
���C=��BAP=45�㣬
�ߡ�APC=��CPN+��APN=90�㣬
��EPF=��APM+��APN=90�㣬
���CPN=��APM��
���CPN�ա�APM��
��S��CPN=S��APM��
��S�ı���PMAN=S��APM+S��APN=S��CPN+S��APN=S��ACP=
| 1 |
| 2 |
| 1 |
| 2 |
���ı���PMAN������������仯���˶�ֵΪ8��
���������⿼������������������������ε����ʺ��ж����������ڽǺͶ���������ֱ�������ε�֪ʶ����ۺ����ã����˷�������˼��ͷ���˼�룬�Ѷ�ƫ��

��ϰ��ϵ�д�
 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ
 ��2013•�����ʼ죩��ͼ����Rt��ABC�У���C=90�㣬��BAC��ƽ����AD��BC�ڵ�D����E��AB��һ�㣬��AEΪֱ���ġ�O����D���ҽ�AC�ڵ�F��
��2013•�����ʼ죩��ͼ����Rt��ABC�У���C=90�㣬��BAC��ƽ����AD��BC�ڵ�D����E��AB��һ�㣬��AEΪֱ���ġ�O����D���ҽ�AC�ڵ�F�� ��ͼ����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm��AD��BD�ֱ��ǡ�BAC�͡�ABC��ƽ���ߣ������ཻ�ڵ�D�����D��BC�ľ��룮
��ͼ����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm��AD��BD�ֱ��ǡ�BAC�͡�ABC��ƽ���ߣ������ཻ�ڵ�D�����D��BC�ľ��룮 �����ƶ���ʹ���30��ǵ����߷ֱ����ABC�ı�AC��BC�ཻ�ڵ�E��F����ʹDEʼ����AB��ֱ��
�����ƶ���ʹ���30��ǵ����߷ֱ����ABC�ı�AC��BC�ཻ�ڵ�E��F����ʹDEʼ����AB��ֱ�� ��ͼ����Rt��ABC�У�BD��AC��sinA=
��ͼ����Rt��ABC�У�BD��AC��sinA= ��P���A���غ�ʱ������P��PQ��AC�ڵ�Q����PQΪ����������PQMN��ʹ��M�����߶�AC�ϣ����P���˶�ʱ��Ϊt��s����
��P���A���غ�ʱ������P��PQ��AC�ڵ�Q����PQΪ����������PQMN��ʹ��M�����߶�AC�ϣ����P���˶�ʱ��Ϊt��s����