题目内容
 如图,直线y=-
如图,直线y=-| 3 |
| 4 |
(1)直接填出两点的坐标:A:
(4,0)
(4,0)
,B:(0,3)
(0,3)
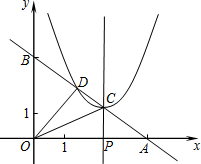
;(2)过点P作直线截△ABO,使截得的三角形与△ABO相似,若当P在某一位置时,满足条件的直线共有4条,t的取值范围是
0<t≤
| 9 |
| 4 |
0<t≤
;| 9 |
| 4 |
(3)如图,过点P作x轴的垂线交直线AB于点C,设以C为顶点的抛物线 y=(x+m)2+n与直线AB的另一交点为D,
①用含t的代数式分别表示m=
-t
-t
,n=-
t+3
| 3 |
| 4 |
-
t+3
;| 3 |
| 4 |
②随着点P运动,CD的长是否为定值?若是,请求出CD长;若不是,说明理由;
③设△COD的OC边上的高为h,请直接写出当t为何值时,h的值最大?
分析:(1)在直线AB的解析式中,令x=0,能得到点B的坐标;令y=0,能得到点A的坐标.
(2)此题需要注意的是“满足条件的直线共有4条”这个条件,这四条直线中,“过P与直线AB平行的直线、过P与y轴平行的直线、过P与直线AB垂直的直线”这三条直线,点P只要在线段OA上就都能满足“截得的三角形与△ABO相似”,所以求t的取值范围,关键要看第四条,即:当∠PBO=∠BAO时,△PBO、△BAO相似,那么此时点P的位置就能确定符合条件的t的最大值,可根据这个思路解答.
(3)①根据直线AB的解析式,用t表示出点C的坐标,而点C是抛物线的顶点,且抛物线的解析式已表示为顶点式,则m、n的值可求;
②联立直线AB与抛物线的解析式,先求出C、D点的坐标,再判断线段CD的长是否为定值;
③由②的结论知CD是定长,那么以CD为底、点O到直线AB的距离为高即可判断出△OCD的面积是一个定值,反过来看,若以OC为底、h为高,那么当OC最短时,h的值最大;在Rt△AOB中,显然只有当OC⊥AB时,OC最大,此时,先由△AOB的面积求出OC的长,然后在Rt△OCA中,由射影定理求出OP的长,则t值可求.
(2)此题需要注意的是“满足条件的直线共有4条”这个条件,这四条直线中,“过P与直线AB平行的直线、过P与y轴平行的直线、过P与直线AB垂直的直线”这三条直线,点P只要在线段OA上就都能满足“截得的三角形与△ABO相似”,所以求t的取值范围,关键要看第四条,即:当∠PBO=∠BAO时,△PBO、△BAO相似,那么此时点P的位置就能确定符合条件的t的最大值,可根据这个思路解答.
(3)①根据直线AB的解析式,用t表示出点C的坐标,而点C是抛物线的顶点,且抛物线的解析式已表示为顶点式,则m、n的值可求;
②联立直线AB与抛物线的解析式,先求出C、D点的坐标,再判断线段CD的长是否为定值;
③由②的结论知CD是定长,那么以CD为底、点O到直线AB的距离为高即可判断出△OCD的面积是一个定值,反过来看,若以OC为底、h为高,那么当OC最短时,h的值最大;在Rt△AOB中,显然只有当OC⊥AB时,OC最大,此时,先由△AOB的面积求出OC的长,然后在Rt△OCA中,由射影定理求出OP的长,则t值可求.
解答:解:(1)直线y=-
x+3中,当x=0时,y=3,即 B(0,3);
当y=0时,x=4,即 A(4,0);
∴A(4,0)、B(0,3).
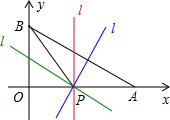 (2)如右图,过P作l∥AB、l⊥OA、l⊥AB时,△PBO、△BAO都相似,此时点P在线段OA上时,都符合要求,所以只考虑第四种情况:
(2)如右图,过P作l∥AB、l⊥OA、l⊥AB时,△PBO、△BAO都相似,此时点P在线段OA上时,都符合要求,所以只考虑第四种情况:
当∠PBO=∠BAO时,Rt△PBO∽Rt△BAO;
易知:tan∠PBO=tan∠BAO=
=
;
在Rt△OBP中,OB=3,则 OP=OB•tan∠PBO=3×
=
∴满足条件的t的取值范围是 0<t≤
.
(3)①由题意,知:P(t,0),则 C(t,-
t+3),而抛物线的顶点坐标为 (-m,n),
∴m=-t,n=-
t+3;
②由①知:y=(x-t)2-
t+3,联立直线AB的解析式,有:
,解得
、
∴点C(t,-
t+3)、D(t-
,-
t+
);
可求得,CD的长为定值,且CD=
;
③由②知:CD的长是定值,且点O到CD的距离不变,所以△OCD的面积是定值;
在△OCD中,以OC为底、h为高,则 S△OCD=
OC•h,S△OCD是定值,所以当OC最短时,h最大;
在Rt△OAB中,OC为底边AB上的高时,OC最短,此时OC⊥AB;
OC=
=
;
在Rt△OAC中,OP=
=
=
;
∴当t=
时,h的值最大.
| 3 |
| 4 |
当y=0时,x=4,即 A(4,0);
∴A(4,0)、B(0,3).
 (2)如右图,过P作l∥AB、l⊥OA、l⊥AB时,△PBO、△BAO都相似,此时点P在线段OA上时,都符合要求,所以只考虑第四种情况:
(2)如右图,过P作l∥AB、l⊥OA、l⊥AB时,△PBO、△BAO都相似,此时点P在线段OA上时,都符合要求,所以只考虑第四种情况:当∠PBO=∠BAO时,Rt△PBO∽Rt△BAO;
易知:tan∠PBO=tan∠BAO=
| OB |
| OA |
| 3 |
| 4 |
在Rt△OBP中,OB=3,则 OP=OB•tan∠PBO=3×
| 3 |
| 4 |
| 9 |
| 4 |
∴满足条件的t的取值范围是 0<t≤
| 9 |
| 4 |
(3)①由题意,知:P(t,0),则 C(t,-
| 3 |
| 4 |
∴m=-t,n=-
| 3 |
| 4 |
②由①知:y=(x-t)2-
| 3 |
| 4 |
|
|
|
∴点C(t,-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 57 |
| 16 |
可求得,CD的长为定值,且CD=
| 15 |
| 16 |
③由②知:CD的长是定值,且点O到CD的距离不变,所以△OCD的面积是定值;
在△OCD中,以OC为底、h为高,则 S△OCD=
| 1 |
| 2 |
在Rt△OAB中,OC为底边AB上的高时,OC最短,此时OC⊥AB;
OC=
| OA•OB |
| AB |
| 12 |
| 5 |
在Rt△OAC中,OP=
| OC2 |
| OA |
(
| ||
| 4 |
| 36 |
| 25 |
∴当t=
| 36 |
| 25 |
点评:此题考查的内容较为繁杂,在(2)题中,找出四条符合条件的直线是解答该题的关键;最后一个小题中,以三角形的面积是定值为跳板来判断OC和h之间的关系是解题的突破口.

练习册系列答案
相关题目
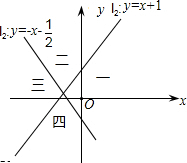 如图,直线l1:y=x+1与直线l2:y=-x-
如图,直线l1:y=x+1与直线l2:y=-x-| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| A、第一部分 | B、第二部分 |
| C、第三部分 | D、第四部分 |
 14、如图,直线AB、CD交于O点,OE为∠AOC的平分线,∠1=17°,则∠2=
14、如图,直线AB、CD交于O点,OE为∠AOC的平分线,∠1=17°,则∠2=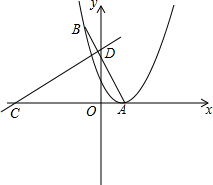 (2012•江汉区模拟)已知:抛物线
(2012•江汉区模拟)已知:抛物线 (2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是
(2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是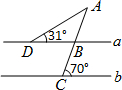 (2012•广州模拟)如图,直线a∥b,则∠A的度数是( )
(2012•广州模拟)如图,直线a∥b,则∠A的度数是( )