题目内容
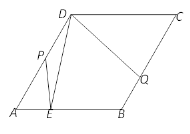
【题目】如图,在菱形![]() 中,
中,![]() =60°, AB=2,点E是AB上的动点,作∠EDQ=60°交BC于点Q,点P在AD上,PD=PE.
=60°, AB=2,点E是AB上的动点,作∠EDQ=60°交BC于点Q,点P在AD上,PD=PE.
(1)求证:AE=BQ;
(2)连接PQ, EQ,当∠PEQ=90°时,求![]() 的值;
的值;
(3)当AE为何值时,△PEQ是等腰三角形.
【答案】(1)见解析;(2)![]() =
=![]() ;(3)AE为
;(3)AE为![]() 或2
或2
【解析】
(1)连结DB,根据“ASA”证明△ADE≌△BDQ即可;
(2)先证明△DEQ是等边三角形,可得∠DEQ=60°,进而可证明∠AED=90°,根据勾股定理求出DE的长,根据两平行线间的距离相等求出PQ的长,即可求出![]() 的值;
的值;
(3)分三种情况讨论求解:①当QP=QE时,②当PE=QE时,③当PE=PQ时.
解:(1)连结DB,
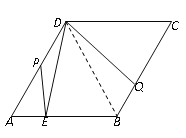
∵四边形ABCD为菱形,∠A=60°,
∴AD=AB=DB,∠DBQ=∠A=60°.
∴∠ADB=60°.
∵∠EDQ=60°,
∴∠ADE=∠BDQ.
∴△ADE≌△BDQ.
∴AE=BQ.
(2)如图,

∵△ADE≌△BDQ,
∴DE=DQ.
∵∠EDQ=60°,
∴△DEQ是等边三角形,
∴∠DEQ=60°,DE=EQ=DQ.
∵∠PEQ=90°,
∴∠PED=30°.
∵PD=PE,
∴∠PDE=∠PED=30°.
∴∠AED=90°.
∵AD=2,
∴DE=![]() .
.
∵PD=PE, EQ=DQ,
∴PQ是DE的中垂线,
∴PQ= AB=2.
∴![]() =
=![]() .
.
(3)①当QP=QE时,如图1,
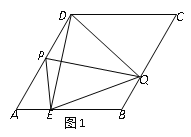
∵∠EQP=∠DQP=30°,
∴∠QPE=∠QEP=∠PDQ =75°.
∴∠PED=∠PDE=15°,
∴∠APE=30°,
∴∠AEP=90°.
∴AP=2AE,PE=PD=![]() AE,
AE,
∴![]() AE+2AE=2,
AE+2AE=2,
∴AE=![]() .
.
②当PE=QE时,
∵△DEQ是正三角形,
∴△PDE是正三角形,∠ADE=60°,
点E
∴AE=2.
③当PE=PQ时,
∵∠EQP=30°,
∴∠PEQ=30°,由图可知∠PEQ≥60°,
∴点E不存在.
综上所述,当AE为![]() 或2时,△PEQ是等腰三角形.
或2时,△PEQ是等腰三角形.