Question

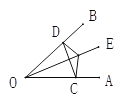
【题目】如图，已知CE⊥AB，垂足为点E，DF⊥AB，垂足为点F，AF=BE，AC=BD，则下列结论：①Rt△AEC≌Rt△BFD；②∠C+∠B=90°；③AC∥BD；④∠A=∠D．

其中正确的结论为____．（填序号）

Answer 1

【答案】①②③

【解析】

由CE⊥AB，DF⊥AB可得△ACE和△BDF都是直角三角形；进而结合AC=BD，可以证明出△ACE≌△BDF；从上面的全等三角形可以得出其中相等的边和角，即可以判断题中正确的选项.

∵CE⊥AB，DF⊥AB

∴△ACE和△BDF都是直角三角形

∵AF=BE，EF公用

∴AE=BF

∵AE=BF，AC=BD，△ACE和△BDF都是直角三角形

∴Rt△AEC≌Rt△BFD

即①正确；

∵Rt△AEC≌Rt△BFD

∴∠CAB=∠ABD

故④错误；

∵在△AEC中，CE⊥AB

∴∠ACE+∠CAB=90°

∵∠ACE+∠CAB=90°，∠CAB=∠ABD

∴∠ACE+∠ABD=90°

故②正确；

∵∠CAB=∠ABD

∴AC∥BD

故③正确.

故答案为：①②③.