题目内容
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.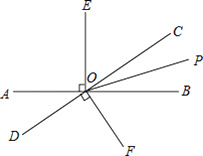
(1)图中除直角外,还有相等的角吗?请写出两对:①;② .
(2)如果∠COP=20°,则①∠BOP=°;②∠POF=°.
(3)∠EOC与∠BOF相等吗? , 理由是 .
(4)如果∠COP=20°,求∠DOE的度数.
【答案】
(1)∠BOP=∠COP,∠AOD=∠BOC
(2)∠BOP=∠COP=20°,∠POF=90°﹣20°=70°
(3)相等,同角的余角相等
(4)解:∵OP是∠BOC的平分线,
∴∠BOC=2×20°=40°,
∴∠AOD=∠BOC=40°,
∴∠DOE=∠AOD+∠AOE,
=40°+90°,
=130°
【解析】解:(1)①∠BOP=∠COP,②∠AOD=∠BOC;
( 2 )①∠BOP=∠COP=20°,②∠POF=90°﹣20°=70°;
( 3 )相等,同角的余角相等;
故答案为:(1)∠BOP=∠COP,∠AOD=∠BOC,(2)20,70,(3)相等,等角的余角相等;
(1)根据角平分线的定义得出①∠BOP=∠COP ;根据对顶角相等得出②∠AOD=∠BOC;
(2)根据角平分线的定义得出①∠BOP=∠COP= 20° ;根据垂直的定义及角的和差得出∠POF=90°﹣20°=70° ;
(3)相等,根据同角的余角相等得出结论 ;
(4)根据角平分线的定义得出∠BOC的度数,根据对顶角相等得出∠AOD=∠BOC=40°,根据垂直的定义及角的和差得出∠DOE=∠AOD+∠AOE,从而得出答案。

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某学校对学生的暑假参加志愿服务时间进行抽样调查,将收集的数据分成A,B,C,D,E五组进行整理,并绘制成如下的统计图表(图中信息不完整).
请结合以上信息解答下列问题
(1)求a、m、n的值.
(2)补全“人数分组统计图①中C组的人数和图②A组和B组的比例值”.
(3)若全校学生人数为800人,请估计全校参加志愿服务时间在30≤x<40的范围的学生人数.
分组统计表
组别 | 志愿服务时间 | 人数 |
A | 0≤x<10 | a |
B | 10≤x<20 | 40 |
C | 20≤x<30 | m |
D | 30≤x<40 | n |
E | x≥40 | 16 |