Question

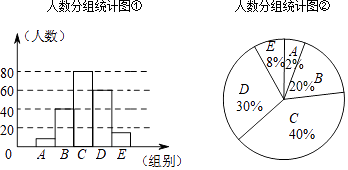
【题目】某学校对学生的暑假参加志愿服务时间进行抽样调查，将收集的数据分成A，B，C，D，E五组进行整理，并绘制成如下的统计图表（图中信息不完整）．

请结合以上信息解答下列问题
（1）求a、m、n的值．
（2）补全“人数分组统计图①中C组的人数和图②A组和B组的比例值”．
（3）若全校学生人数为800人，请估计全校参加志愿服务时间在30≤x＜40的范围的学生人数．
分组统计表

组别	志愿服务时间 x（时）	人数
A	0≤x＜10	a
B	10≤x＜20	40
C	20≤x＜30	m
D	30≤x＜40	n
E	x≥40	16

Answer 1

【答案】
（1）解：∵本次调查的总人数为16÷8%=200（人），

则m=200×40%=80，n=200×30%=60，

∴a=200﹣（40+80+60+16）=4；

（2）解：A组的百分比为 ×100%=2%，B组百分比为 ×100%=20%，

补全统计图如下：

（3）解：估计全校参加志愿服务时间在30≤x＜40的范围的学生人数为800×30%=240（人）．
【解析】（1）首先依据总人数=频数÷百分比可求得总人数，然后，再用总人数乘以C、D组的百分比可分别求得m、n的值，最后，根据各组人数之和等于总人数可得a的值；
（2）依据百分比=频数÷总人数可求得A、B组的百分比，结合（1）中所求数据可补全统计图；
（3）先可估计出总体中D组所占的百分比，然后用总人数乘以样本中D组的百分比可得.
【考点精析】利用频数分布直方图和扇形统计图对题目进行判断即可得到答案，需要熟知特点：①易于显示各组的频数分布情况；②易于显示各组的频数差别．（注意区分条形统计图与频数分布直方图）；能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况．