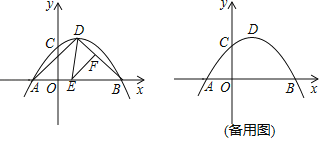题目内容
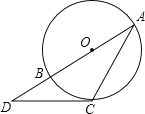
【题目】已知:四边形ABCD内接于⊙O,∠ADC=90°,DE⊥AB,垂足为点E,DE的锯长线交⊙O于点F,DC的延长线与FB的延长线交于点G.
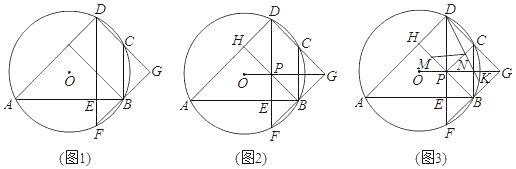
(1)如图1,求证:GD=GF;
(2)如图2,过点B作BH⊥AD,垂足为点M,B交DF于点P,连接OG,若点P在线段OG上,且PB=PH,求∠ADF的大小;
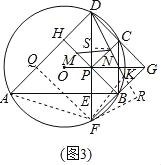
(3)如图3,在(2)的条件下,点M是PH的中点,点K在![]() 上,连接DK,PC,D交PC点N,连接MN,若AB=12
上,连接DK,PC,D交PC点N,连接MN,若AB=12![]() ,HM+CN=MN,求DK的长.
,HM+CN=MN,求DK的长.
【答案】(1)见解析;(2)∠ADF=45°;(3)![]() .
.
【解析】
(1)利用“同圆中,同弧所对的圆周角相等”可得∠A=∠GFD,由“等角的余角相等”可得∠A=∠GDF,等量代换得∠GDF=∠GFD,根据“三角形中,等角对等边”得GD=GF;
(2)连接OD、OF,由△DPH≌△FPB可得:∠GBH=90°,由四边形内角和为360°可得:∠G=90°,即可得:∠ADF=45°;
(3)由等腰直角三角形可得AH=BH=12,DF=AB=12![]() ,由四边形ABCD内接于⊙O,可得:∠BCG=45°=∠CBG,GC=GB,可证四边形CDHP是矩形,令CN=m,利用勾股定理可求得m=2,过点N作NS⊥DP于S,连接AF,FK,过点F作FQ⊥AD于点Q,过点F作FR⊥DK交DK的延长线于点R,通过构造直角三角形,应用解直角三角形方法球得DK.
,由四边形ABCD内接于⊙O,可得:∠BCG=45°=∠CBG,GC=GB,可证四边形CDHP是矩形,令CN=m,利用勾股定理可求得m=2,过点N作NS⊥DP于S,连接AF,FK,过点F作FQ⊥AD于点Q,过点F作FR⊥DK交DK的延长线于点R,通过构造直角三角形,应用解直角三角形方法球得DK.
解:(1)证明:∵DE⊥AB
∴∠BED=90°
∴∠A+∠ADE=90°
∵∠ADC=90°
∴∠GDF+∠ADE=90°
∴∠A=∠GDF
∵![]()
∴∠A=∠GFD
∴∠GDF=∠GFD
∴GD=GF
(2)连接OD、OF
∵OD=OF,GD=GF
∴OG⊥DF,PD=PF
在△DPH和△FPB中
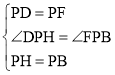
∴△DPH≌△FPB(SAS)
∴∠FBP=∠DHP=90°
∴∠GBH=90°
∴∠DGF=360°﹣90°﹣90°﹣90°=90°
∴∠GDF=∠DFG=45°
∴∠ADF=45°
(3)在Rt△ABH中,∵∠BAH=45°,AB=12![]()
∴AH=BH=12
∴PH=PB=6
∵∠HDP=∠HPD=45°
∴DH=PH=6
∴AD=12+6=18,PN=HM=![]() PH=3,PD=6
PH=3,PD=6![]()
∵∠BFE=∠EBF=45°
∴EF=BE
∵∠DAE=∠ADE=45°
∴DE=AE
∴DF=AB=12![]()
∵四边形ABCD内接于⊙O
∴∠DAB+∠BCD=180°
∴∠BCD=135°
∴∠BCG=45°=∠CBG
∴GC=GB
又∵∠CGP=∠BGP=45°,GP=GP
∴△GCP≌△GBP(SAS)
∴∠PCG=∠PBG=90°
∴∠PCD=∠CDH=∠DHP=90°
∴四边形CDHP是矩形
∴CD=HP=6,PC=DH=6,∠CPH=90°
令CN=m,则PN=6﹣m,MN=m+3
在Rt△PMN中,∵PM2+PN2=MN2
∴32+(6﹣m)2=(m+3)2,解得m=2
∴PN=4
过点N作NS⊥DP于S,
在Rt△PSN中,PS=SN=2![]()
DS=6![]() ﹣2
﹣2![]() =4
=4![]()
![]()
连接AF,FK,过点F作FQ⊥AD于点Q,过点F作FR⊥DK交DK的延长线于点R
在Rt△DFQ中,FQ=DQ=12
∴AQ=18﹣12=6
∴tan![]()
∵四边形AFKD内接于⊙O,
∴∠DAF+∠DKF=180°
∴∠DAF=180°﹣∠DKF=∠FKR
在Rt△DFR中,∵DF=![]()
∴![]()
在Rt△FKR中,∵FR=![]() tan∠FKR=2
tan∠FKR=2
∴KR=![]()
∴DK=DR﹣KR=![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案