题目内容
【题目】如图,直线![]() 与双曲线
与双曲线![]() 在第一象限内交于
在第一象限内交于![]() 两点,已知
两点,已知![]() .
.

(1)求![]() 的值及直线
的值及直线![]() 的解析式.
的解析式.
(2)根据函数图象,直接写出不等式![]() 的解集.
的解集.
(3)设点是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 的面积为
的面积为![]() 时,请直接写出此时点
时,请直接写出此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() (2)解集为
(2)解集为![]() 或
或![]() (3)
(3)![]()
【解析】
(1)先把B(2,1)代入![]() ,求出反比例函数解析式,进而求出点A坐标,最后用待定系数法,即可得出直线AB的解析式;
,求出反比例函数解析式,进而求出点A坐标,最后用待定系数法,即可得出直线AB的解析式;
(2)直接利用函数图象得出结论;
(3)先设出点P坐标,进而表示出△PED的面积等于![]() ,解之即可得出结论.
,解之即可得出结论.
解:(1):∵点![]() 在双曲线
在双曲线![]() 上,
上,
∴![]() ,
,
∴双曲线的解析式为![]() .
.
∵![]() 在双曲线
在双曲线![]() ,
,
∴![]() ,
,
∴![]() .
.
∵直线![]() 过
过![]() 两点,
两点,
∴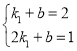 ,解得
,解得![]()
∴直线![]() 的解析式为
的解析式为![]()
(2)根据函数图象,由不等式与函数图像的关系可得:
双曲线在直线上方的部分对应的x范围是:![]() 或
或![]() ,
,
∴不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(3)点![]() 的坐标为
的坐标为![]() .
.
设点![]() ,且
,且![]() ,
,
则![]() .
.
∵当![]() 时,
时,
解得![]() ,
,
∴此时点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目
【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
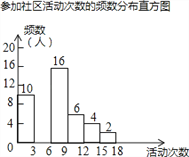
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | m | b |
15<x≤18 | 2 | n |
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?