题目内容
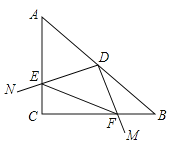
【题目】如图，在Rt△ABC 中，∠C=90°，AC=BC，AB=8，点D为AB的中点，若直角MDN绕点D旋转分别交AC于点E，交BC于点F，则下列说法：①AE="CF" ②EC+CF=
③DE="DF" ④若△ECF的面积为一个定值，则EF的长也是一个定值，其中正确的是（ ）
A.①②B.①③C.①②③D.①②③④
【答案】D
【解析】
试题连接CD，在Rt△ABC 中，∠C=90°，AC=BC，点D为AB的中点由等腰三角形的“三线合一”，
得到AD=DB=CD=4，∠ACD=∠B=45°，∠CDB=90°又因为∠NDM=90°,易得∠NDC=∠BDM，所以
所以AE=CF；DE=DF；所以EC+CF=AC=
；
因为面积是个定值，所以CF不变，则CE不变，由直角三角形勾股定理的EF不变.
所以选D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
