题目内容
【题目】如图,在半径为5的⊙![]() 中,弦
中,弦![]() ,
,![]() 是弦
是弦![]() 所对的优弧上的动点,连接
所对的优弧上的动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交射线
的垂线交射线![]() 于点
于点![]() ,当
,当![]() 是以
是以![]() 为腰的等腰三角形时,线段
为腰的等腰三角形时,线段![]() 的长为_____.
的长为_____.
【答案】8或![]()
【解析】
根据题意,以![]() 为腰的等腰三角形有两种情况,当AB=AP时,利用垂径定理及相似三角形的性质列出比例关系求解即可,当AB=BP时,通过角度运算,得出BC=AB=8即可.
为腰的等腰三角形有两种情况,当AB=AP时,利用垂径定理及相似三角形的性质列出比例关系求解即可,当AB=BP时,通过角度运算,得出BC=AB=8即可.
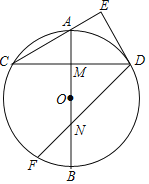
解:①当AB=AP时,如图,连接OA、OB,延长AO交BP于点G,故AG⊥BP, 过点O作OH⊥AB于点H,
∵在同圆或等圆中,同弧所对的圆周角等于圆心角的一半,
∴![]() ,
,
由垂径定理可知![]() ,
,![]()
∴![]() ,
,
在Rt△OAH中,![]()
在Rt△CAP中,![]() ,且
,且![]()
∴![]() ,
,
在Rt△PAG与Rt△PCA中,∠GPA=∠APC,∠PGA=∠PAC,
∴Rt△PAG∽Rt△PCA
∴![]() ,则
,则![]() ,
,
∴![]() ;
;
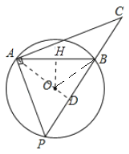
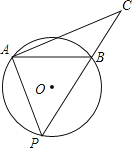
②当AB=BP时,如下图所示,∠BAP=∠BPA,
∴在Rt△PAC中,∠C=90°-∠BPA=90°-∠BAP=∠CAB,
∴BC=AB=8
故答案为8或![]()

练习册系列答案
相关题目
【题目】某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如图的统计表和扇形图:

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 20 |
B | b | 18 |
C | c | 15 |
(1)①在扇形图中,a= ,C部门所对应的圆心角的度数为 .
②在统计表中,b= ,c= .
(2)求这个公司平均每人所创年利润.