题目内容
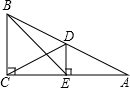
已知:如图,将长方形纸片沿着CE所在直线对折,B点落在点B′处,CD与EB′交于点F,如果AB=10cm,AD=6cm,AE=2cm,求EF的长.


根据题意,∠CEF=∠CEB,
∵AB∥CD,
∴∠CEB=∠ECD,
∴∠CEF∠ECD,
∴EF=CF,
过E作EG⊥CD于G,
设EF=CF=x,
则GF=AB-AE-EF=10-2-x=8-x,
在Rt△EFG中,EF2=GF2+EG2,
∴x2=(8-x)2+62,
∴x=
,
∴EF=
cm.

∵AB∥CD,
∴∠CEB=∠ECD,
∴∠CEF∠ECD,
∴EF=CF,
过E作EG⊥CD于G,
设EF=CF=x,
则GF=AB-AE-EF=10-2-x=8-x,
在Rt△EFG中,EF2=GF2+EG2,
∴x2=(8-x)2+62,
∴x=
| 25 |
| 4 |
∴EF=
| 25 |
| 4 |


练习册系列答案
相关题目
 连接AE.
连接AE.